Chapter 18
Kolmogorov-Arnolds Networks (KANs)
"Every sufficiently complex function can be decomposed into simpler, more interpretable components—this is the power of networks like KANs in making sense of high-dimensional data." — Yann LeCun
Chapter 18 of DLVR introduces Kolmogorov-Arnolds Networks (KANs), a powerful approach to function approximation based on the Kolmogorov-Arnold representation theorem, which asserts that any multivariate continuous function can be expressed as a superposition of univariate functions. This chapter begins by explaining the theoretical foundation of KANs, highlighting their ability to decompose high-dimensional functions into sums of one-dimensional functions, offering an efficient way to address the curse of dimensionality. It delves into the architecture of KANs, discussing the role of layers, activation functions, and the design choices that allow these networks to serve as universal approximators. The chapter also explores different KAN architectures, including deep KANs, and examines the impact of various basis functions on model performance. Training and optimization techniques are thoroughly covered, focusing on gradient-based methods, initialization strategies, and the challenges of optimizing both univariate function parameters and composition structures. The chapter concludes with a discussion on the practical applications of KANs, from scientific computing to high-dimensional regression tasks, providing Rust-based examples and comparisons with traditional models, and emphasizing the potential of KANs to model complex systems with high accuracy and interpretability.
18.1. Introduction to KANs
Kolmogorov-Arnolds Networks (KANs) stem from a profound theoretical insight provided by the Kolmogorov-Arnold representation theorem, which reshaped the understanding of function approximation in high-dimensional spaces. This theorem, initially formulated by Andrey Kolmogorov and refined by Vladimir Arnold, states that any continuous multivariate function $f: \mathbb{R}^n \rightarrow \mathbb{R}$ can be represented as a sum of continuous univariate functions. Formally, the theorem asserts that for any continuous function $f$ over $n$ variables, there exist continuous functions $\phi$ and $\psi$ such that:
$$ f(x_1, x_2, \ldots, x_n) = \sum_{q=1}^{2n+1} \psi_q \left( \sum_{i=1}^n \phi_{qi}(x_i) \right). $$
In this formulation, the functions $\phi_{qi}$ and $\psi_q$ are univariate functions, which means they each depend on only a single variable. This decomposition allows a complex, high-dimensional function to be expressed as a combination of simpler, one-dimensional transformations. The theorem provides a theoretical underpinning for KANs, suggesting that even intricate relationships among variables can be captured using a layered approach that decomposes the problem into simpler components.
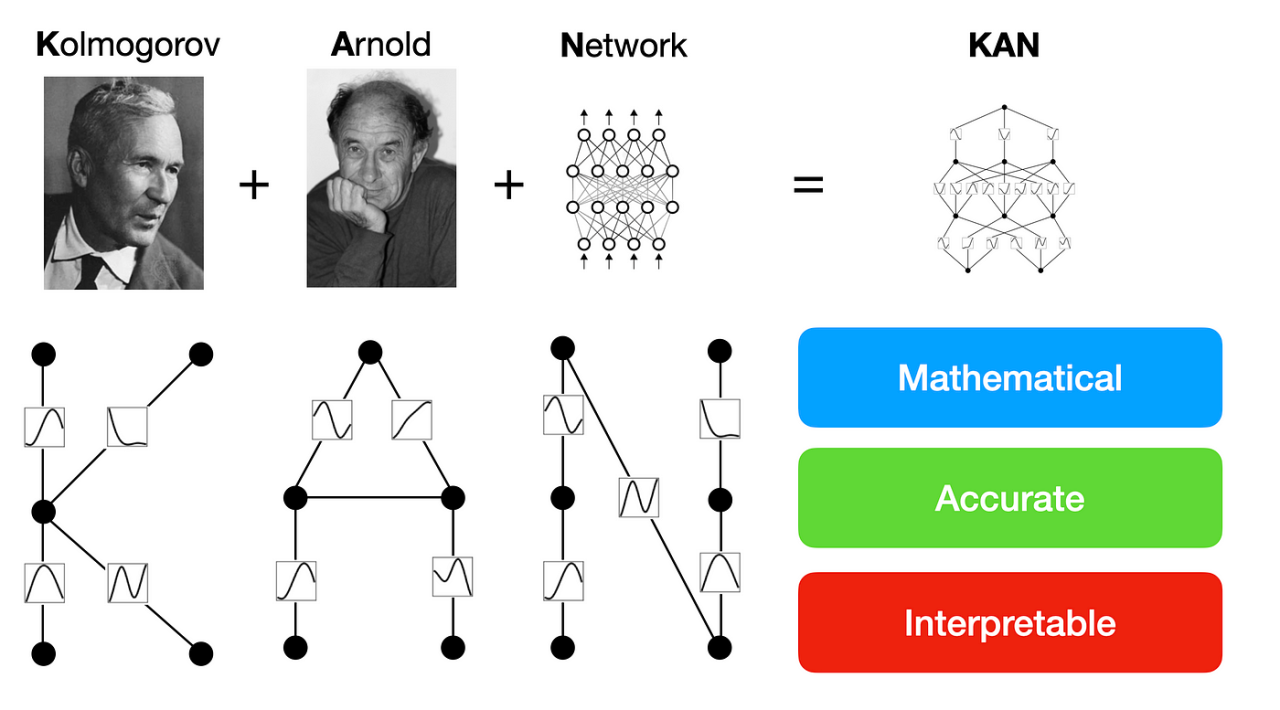
Figure 1: Key concept of KAN model.
The power of this representation lies in its ability to address the curse of dimensionality—a critical challenge in machine learning and numerical analysis. The curse of dimensionality refers to the exponential increase in computational complexity as the number of input dimensions grows, often making high-dimensional problems intractable with traditional methods. KANs, by decomposing the target function into sums of univariate functions, mitigate this complexity. Each univariate function captures the variation along a single input dimension, while the sum of these functions reconstructs the original high-dimensional behavior. As a result, KANs can efficiently approximate complex functions without the massive computational overhead typical of models that attempt to directly learn interactions across all dimensions.
In the context of deep learning, KANs extend the concept of universal approximation, which is central to neural network theory. Universal approximation refers to the ability of neural networks to approximate any continuous function, given enough hidden units or layers. KANs achieve this in a structured way, leveraging the Kolmogorov-Arnold decomposition to build networks that specifically focus on capturing one-dimensional variations before combining them. This structure makes KANs particularly well-suited for problems where the relationship between variables is complex but continuous, such as modeling physical phenomena, financial time series, or other scientific data.
The architecture of KANs reflects this decomposition. Each layer in a KAN corresponds to a stage in the function decomposition. The inner layers approximate the univariate functions $\phi_{qi}(x_i)$, where each $\phi_{qi}$ maps one input dimension to an intermediate representation. These representations are then aggregated using the outer layers, which correspond to the $\psi_q$ functions that synthesize the output from these intermediate forms. This design allows KANs to represent the original multivariate function through the composition of simpler functions, aligning closely with the theoretical basis of the Kolmogorov-Arnold theorem. The use of smooth activation functions, such as the hyperbolic tangent (tanh) or Gaussian functions, ensures that the approximation remains continuous, adhering to the theorem’s requirement of continuity.
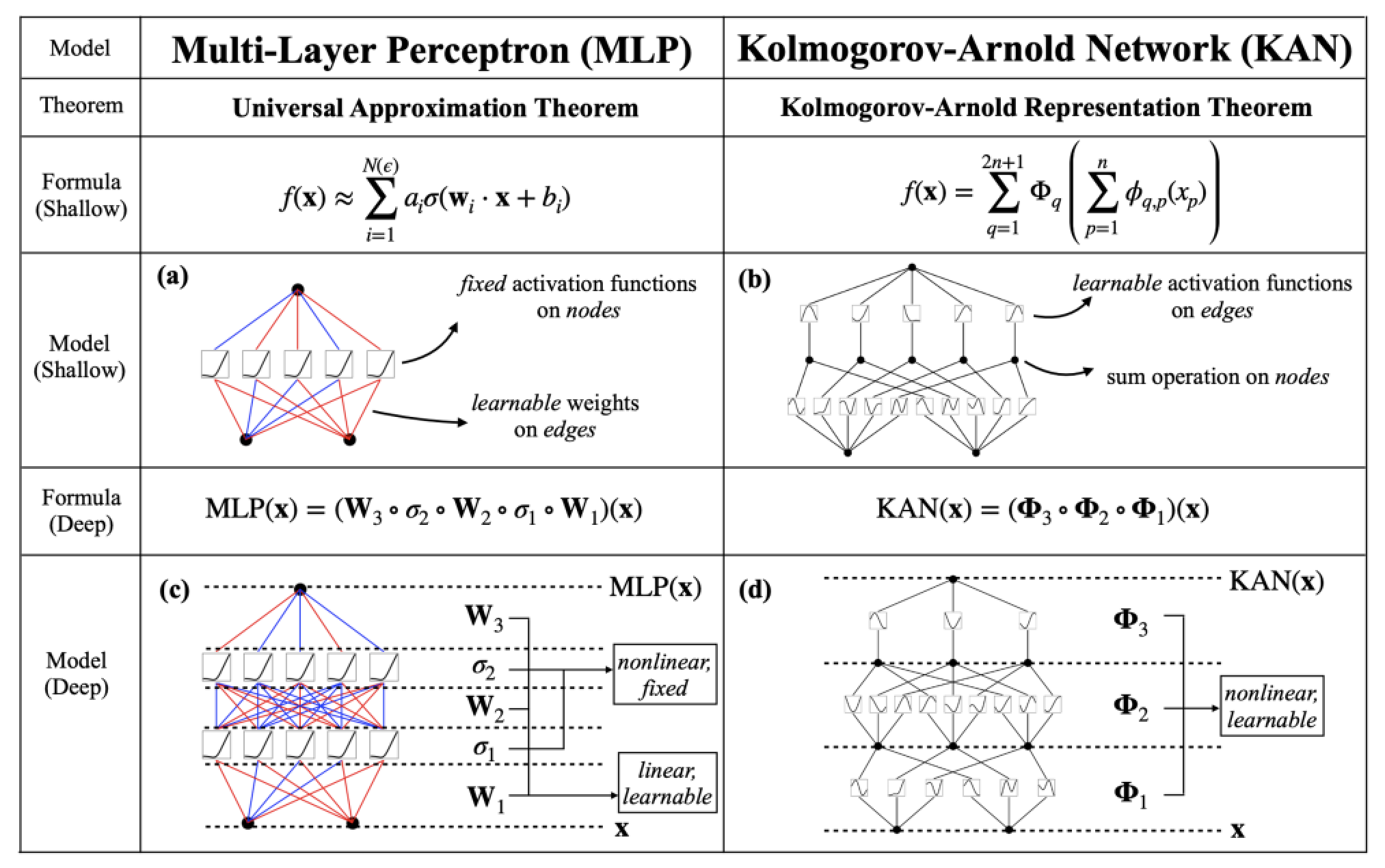
Figure 2: Comparison between MLP and KAN.
KAN and MLP are both function approximators in machine learning, yet they are built on different theoretical foundations, use distinct mathematical formulations, and differ in their model architectures. Understanding these differences provides insight into when and how each approach should be applied.
KANs are grounded in the Kolmogorov-Arnold representation theorem, which asserts that any continuous multivariate function can be expressed as a superposition of continuous univariate functions. Specifically, for any function $f(x_1, x_2, \dots, x_n)$, there exist continuous univariate functions $\phi_i$ and combining functions $\psi$ such that the function can be written as $f(x_1, x_2, \dots, x_n) = \sum_{q=1}^{2n+1} \psi_q \left( \sum_{i=1}^{n} \phi_{qi}(x_i) \right)$. This theorem provides the foundation for KANs, which approximate complex multivariate functions by decomposing them into sums of simpler univariate functions. In contrast, MLPs rely on the universal approximation theorem, which states that a feedforward neural network with a single hidden layer and nonlinear activation functions can approximate any continuous function on a compact subset of $\mathbb{R}^n$. The universal approximation theorem does not decompose the function like the Kolmogorov-Arnold theorem but shows that neural networks are powerful enough to approximate complex functions with sufficient neurons.
In terms of mathematical formulation, a shallow KAN adheres closely to the Kolmogorov-Arnold decomposition. The function $f(x_1, x_2, \dots, x_n)$ is approximated by applying univariate functions $\phi_{qi}(x_i)$ to each input variable and then combining these with the functions $\psi_q$. Mathematically, this looks like $f(x_1, x_2, \dots, x_n) = \sum_{q=1}^{2n+1} \psi_q \left( \sum_{i=1}^{n} \phi_{qi}(x_i) \right)$. A deep KAN builds on this by introducing multiple layers of transformations, where each layer applies univariate transformations at a progressively deeper level. In this formulation, the function can be written as $f(x_1, x_2, \dots, x_n) = \sum_{q=1}^{2n+1} \psi_q^{(k)} \left( \sum_{i=1}^{n} \phi_{qi}^{(k-1)} \left( \dots \phi_{qi}^{(1)}(x_i) \right) \right)$ refers to the transformations at each successive layer. This deep structure allows KANs to approximate more complex relationships by refining the input transformation across multiple layers.
On the other hand, a shallow MLP consists of an input layer, a single hidden layer, and an output layer. The function $f(x)$ in this case is represented as $f(x) = \sigma_2(W_2 \sigma_1(W_1 x + b_1) + b_2)$, where $W_1$ and $W_2$ are weight matrices, $b_1$ and $b_2$ are biases, and $\sigma_1$ and $\sigma_2$ are nonlinear activation functions such as ReLU or sigmoid. The deep version of an MLP introduces multiple hidden layers, allowing the network to capture more abstract and complex representations of the input data. In this case, the function becomes $f(x) = \sigma_L(W_L \sigma_{L-1}( \dots \sigma_2(W_2 \sigma_1(W_1 x + b_1) + b_2) \dots ) + b_L)$, where $L$ represents the number of layers. This deeper structure enables MLPs to learn hierarchical representations, where each layer builds on the features extracted by the previous layer.
The model architecture of KANs is directly related to the Kolmogorov-Arnold decomposition, making it interpretable. A shallow KAN implements the theorem by transforming each input variable independently using univariate functions and then combining them to approximate the output. This decomposition is explicit, allowing one to see how each variable contributes to the final prediction. A deep KAN extends this by stacking multiple layers of univariate transformations, allowing the model to capture more intricate relationships between variables, making it useful for more complex tasks. The deeper structure increases the flexibility of KANs while maintaining their decompositional nature, which can be beneficial in domains requiring detailed insights into variable interactions, such as scientific computing or control systems.
In contrast, shallow MLPs and deep MLPs use fully connected layers where each neuron in one layer is connected to every neuron in the next layer. This structure is highly flexible and can model a wide range of functions, but it is less interpretable than KANs because the transformations applied to the inputs are not easily decomposable into meaningful components. Deep MLPs, with multiple hidden layers, can learn complex patterns and hierarchical representations of data, making them suitable for tasks such as image recognition and natural language processing, where abstract feature extraction is crucial.
Overall, KANs are well-suited for tasks that require a clear and interpretable decomposition of the input features, such as scientific modeling and control systems. MLPs, by contrast, are more widely used in machine learning applications due to their flexibility and ability to capture complex, hierarchical patterns in data. However, this comes at the cost of interpretability, especially in deeper networks where the relationships between inputs and outputs become less transparent. While KANs provide an explicit mathematical decomposition based on the Kolmogorov-Arnold theorem, MLPs rely on the universal approximation theorem, focusing more on the network's capacity to approximate functions through the learning of weights and biases.\
\
The practical implementation of KANs using Rust involves creating an environment that leverages Rust's strengths in memory safety and concurrency, which are essential for handling the intensive computations required for training deep learning models. Libraries like tch-rs, which provides bindings to PyTorch, and burn, which helps with structuring neural network layers, facilitate the construction of KANs. The implementation of a basic KAN model begins with defining the layers that approximate the univariate functions $\phi_{qi}$. These layers are followed by aggregation layers that represent the $\psi_q$ functions, which sum the contributions of each input dimension to produce the final output.
For example, one might construct a KAN to approximate a nonlinear function like $f(x_1, x_2) = \sin(x_1) \cdot \cos(x_2)$. In this implementation, the inner layers of the KAN learn to approximate the sine and cosine components as univariate functions of $x_1$ and $x_2$, respectively. The outer layers then combine these approximations to reconstruct the product of the two functions, aiming to match the target function's behavior. Training involves defining a loss function—such as Mean Squared Error (MSE)—to measure how closely the KAN's output matches the desired output across a range of input values. Optimizers like Adam or stochastic gradient descent (SGD) adjust the parameters of the model, refining the univariate function approximations and their combination.
In industry, KANs offer a powerful tool for domains where understanding variable interactions is as crucial as achieving high predictive accuracy. For example, in financial modeling, decomposing complex market behaviors into simpler trends can provide insights into how individual factors drive overall performance. Similarly, in robotics and control systems, where understanding the role of each control variable is vital, KANs can provide a more interpretable model of how inputs map to desired outcomes. The ability of KANs to decompose functions makes them particularly valuable in scenarios where models need to be both accurate and interpretable, such as in healthcare for modeling physiological systems or in energy management for understanding the relationship between environmental variables and energy consumption.
Using Rust for these implementations not only ensures the models' performance but also benefits from Rust’s focus on safety and concurrency, allowing efficient parallelization of training processes. This is particularly important in scientific computing, where simulations often require both precision and speed. With Rust, developers can optimize tensor operations, directly control memory usage, and manage parallel processing, making it possible to deploy KANs in resource-intensive environments. As a result, Rust offers a robust platform for realizing the theoretical potential of KANs, bridging the gap between mathematical elegance and practical application in high-dimensional function approximation.
This Rust code compares two types of neural networks, KAN and MLP, on a synthetic dataset for a regression task. The goal is to implement both models using the tch-rs crate, train them on the same dataset, and evaluate their performance in terms of mean squared error (MSE). The dataset is generated within the code, where the relationship between the input and output follows a cubic function with noise, simulating a typical regression scenario. The KAN model uses a polynomial basis to transform the inputs, while the MLP model relies on a simple fully connected architecture. After training, the models are compared to determine which performs better at approximating the underlying function.
use tch::{nn, nn::Module, nn::OptimizerConfig, Device, Tensor, Kind};
// Generate a synthetic dataset for regression
fn generate_synthetic_data(n_samples: i64) -> (Tensor, Tensor, Tensor, Tensor) {
let x = Tensor::randn(&[n_samples, 1], (Kind::Float, Device::Cpu)); // Random inputs
let y: Tensor = x.pow_tensor_scalar(3.0) + 0.5 * x.pow_tensor_scalar(2.0)
+ 0.1 * Tensor::randn(&[n_samples, 1], (Kind::Float, Device::Cpu)); // Cubic relationship with noise
let train_size = (n_samples * 80 / 100) as i64;
let train_x = x.narrow(0, 0, train_size);
let train_y = y.narrow(0, 0, train_size);
let test_x = x.narrow(0, train_size, n_samples - train_size);
let test_y = y.narrow(0, train_size, n_samples - train_size);
(train_x, train_y, test_x, test_y)
}
// Define a polynomial basis function for use in KAN models
fn polynomial_basis(x: &Tensor, degree: i64) -> Tensor {
let mut result = Tensor::ones_like(x);
for d in 1..=degree {
result = result + x.pow_tensor_scalar(d as f64);
}
result
}
// Define a shallow KAN model using a specified basis function
fn shallow_kan(vs: &nn::Path, degree: i64) -> impl Module {
nn::seq()
.add_fn(move |x| polynomial_basis(x, degree)) // Move the degree into the closure
.add(nn::linear(vs / "layer1", 1, 32, Default::default()))
.add_fn(|x| x.relu())
.add(nn::linear(vs / "output", 32, 1, Default::default()))
}
// Define a simple MLP for regression
fn mlp(vs: &nn::Path, input_size: i64, hidden_size: i64) -> impl Module {
nn::seq()
.add(nn::linear(vs / "layer1", input_size, hidden_size, Default::default()))
.add_fn(|x| x.relu())
.add(nn::linear(vs / "output", hidden_size, 1, Default::default()))
}
// Train a model on the dataset
fn train_model<M: Module>(
model: &M,
train_x: &Tensor,
train_y: &Tensor,
vs: &nn::VarStore,
num_epochs: i64,
learning_rate: f64,
) -> f64 {
let mut opt = nn::Adam::default().build(vs, learning_rate).unwrap();
for epoch in 1..=num_epochs {
let logits = model.forward(&train_x);
let loss = logits.mse_loss(&train_y, tch::Reduction::Mean);
opt.backward_step(&loss);
if epoch % 10 == 0 {
println!("Epoch: {} - Loss: {:.4}", epoch, loss.double_value(&[]));
}
}
model
.forward(&train_x)
.mse_loss(&train_y, tch::Reduction::Mean)
.double_value(&[])
}
// Evaluate the model on test data
fn evaluate_model<M: Module>(model: &M, test_x: &Tensor, test_y: &Tensor) -> f64 {
let predictions = model.forward(&test_x);
predictions
.mse_loss(&test_y, tch::Reduction::Mean)
.double_value(&[])
}
fn main() {
let device = Device::cuda_if_available();
let (train_x, train_y, test_x, test_y) = generate_synthetic_data(500);
// Parameters for training
let num_epochs = 100;
let learning_rate = 0.01;
let hidden_size = 32;
// Training and evaluating KAN model
let kan_vs = nn::VarStore::new(device);
let kan_model = shallow_kan(&kan_vs.root(), 3);
println!("Training KAN...");
let kan_final_loss = train_model(&kan_model, &train_x, &train_y, &kan_vs, num_epochs, learning_rate);
let kan_test_mse = evaluate_model(&kan_model, &test_x, &test_y);
println!("KAN Final Training Loss: {:.4}", kan_final_loss);
println!("KAN Test MSE: {:.4}", kan_test_mse);
// Training and evaluating MLP model
let mlp_vs = nn::VarStore::new(device);
let mlp_model = mlp(&mlp_vs.root(), 1, hidden_size);
println!("\nTraining MLP...");
let mlp_final_loss = train_model(&mlp_model, &train_x, &train_y, &mlp_vs, num_epochs, learning_rate);
let mlp_test_mse = evaluate_model(&mlp_model, &test_x, &test_y);
println!("MLP Final Training Loss: {:.4}", mlp_final_loss);
println!("MLP Test MSE: {:.4}", mlp_test_mse);
// Compare results
if kan_test_mse < mlp_test_mse {
println!("\nKAN outperformed MLP with a lower test MSE!");
} else {
println!("\nMLP outperformed KAN with a lower test MSE!");
}
}
The code begins by generating synthetic data with a cubic relationship and splits it into training and test sets. The KAN model is defined using a polynomial basis function of degree 3, allowing it to decompose the input into simpler univariate components before applying transformations through hidden layers. The MLP model, on the other hand, is a standard feedforward neural network with one hidden layer. Both models are trained using the Adam optimizer, and the MSE is used as the loss function for regression. The code trains both models over 100 epochs, printing the training loss every 10 epochs, and then evaluates their performance on the test data. The final test MSEs are compared, and the model with the lower error is identified as the better performing one. This allows a direct comparison between the interpretability and performance of KANs and the flexibility of MLPs in a regression task.
The code demonstrates training two regression models—a shallow KAN and a standard MLP —on a synthetic dataset. The synthetic dataset is generated with a cubic relationship between input features and the target values, incorporating noise to simulate real-world conditions. The KAN model uses a polynomial basis function to transform input features into a richer representation before training, while the MLP operates directly on the raw input. Both models are trained using Mean Squared Error (MSE) loss with the Adam optimizer. After training, the models are evaluated on a test set to compute their respective test MSEs, providing a measure of their predictive performance. The results are then compared to determine which model better fits the data.
The results show the training loss and test MSE for both the KAN and MLP models. The KAN typically benefits from the polynomial basis function, allowing it to capture non-linear patterns in the data more effectively, which can result in a lower test MSE compared to the MLP. However, if the dataset is simple or the MLP is sufficiently large, the MLP might outperform the KAN due to its general-purpose architecture. The comparison highlights the trade-offs between the specialized feature transformation in KANs and the flexible learning capabilities of MLPs. Whether the KAN or MLP performs better depends on the dataset's complexity and the appropriateness of the polynomial basis function.
Now lets do for classification task. The following Rust code compares KAN and MLP on a synthetic dataset for a binary classification task. The dataset is generated within the code and consists of two-dimensional input features with linearly separable classes. The goal is to implement both the KAN and MLP models, train them on the same dataset, and evaluate their classification performance by comparing their accuracy on unseen test data.
use tch::{nn, nn::Module, nn::OptimizerConfig, Device, Tensor, Kind};
// Generate a synthetic dataset for classification
fn generate_synthetic_classification_data(n_samples: i64) -> (Tensor, Tensor, Tensor, Tensor) {
let x = Tensor::randn(&[n_samples, 2], (Kind::Float, Device::Cpu)); // Random 2D inputs
let labels = (x.slice(1, 0, 1, 1) + x.slice(1, 1, 2, 1))
.ge(0.0)
.to_kind(Kind::Int64)
.squeeze(); // Ensure labels are 1D
let train_size = (n_samples * 80 / 100) as i64;
let train_x = x.narrow(0, 0, train_size);
let train_labels = labels.narrow(0, 0, train_size);
let test_x = x.narrow(0, train_size, n_samples - train_size);
let test_labels = labels.narrow(0, train_size, n_samples - train_size);
// Optional: Verify shapes
println!("train_x shape: {:?}", train_x.size());
println!("train_labels shape: {:?}", train_labels.size());
println!("test_x shape: {:?}", test_x.size());
println!("test_labels shape: {:?}", test_labels.size());
(train_x, train_labels, test_x, test_labels)
}
// Define a polynomial basis function for use in KAN models
fn polynomial_basis(x: &Tensor, degree: i64) -> Tensor {
let mut result = x.shallow_clone(); // Start with the original features
for d in 2..=degree {
result = Tensor::cat(&[result, x.pow_tensor_scalar(d as f64)], 1); // Concatenate higher-order terms
}
result
}
// Define a shallow KAN model using a specified basis function
fn shallow_kan(vs: &nn::Path, degree: i64, num_features: i64) -> impl Module {
let input_size = num_features * degree; // Adjust input size based on basis expansion
nn::seq()
.add_fn(move |x| polynomial_basis(x, degree)) // Use polynomial basis
.add(nn::linear(
vs / "layer1",
input_size,
32,
Default::default(),
))
.add_fn(|x| x.relu())
.add(nn::linear(
vs / "output",
32,
2,
Default::default(),
)) // Output 2 classes for classification
}
// Define a simple MLP for classification
fn mlp(vs: &nn::Path, input_size: i64, hidden_size: i64) -> impl Module {
nn::seq()
.add(nn::linear(
vs / "layer1",
input_size,
hidden_size,
Default::default(),
))
.add_fn(|x| x.relu())
.add(nn::linear(
vs / "output",
hidden_size,
2,
Default::default(),
)) // Output 2 classes for classification
}
// Train a model on the dataset with weight decay (regularization)
fn train_model<M: Module>(
model: &M,
train_x: &Tensor,
train_labels: &Tensor,
vs: &nn::VarStore,
num_epochs: i64,
learning_rate: f64,
) -> f64 {
let mut opt = nn::Adam {
wd: 1e-4,
..Default::default()
}
.build(vs, learning_rate)
.unwrap(); // Add weight decay
for epoch in 1..=num_epochs {
let logits = model.forward(train_x);
let loss = logits.cross_entropy_for_logits(train_labels);
opt.backward_step(&loss);
if epoch % 10 == 0 {
println!(
"Epoch: {} - Loss: {:.4}",
epoch,
loss.double_value(&[])
);
}
}
model
.forward(train_x)
.cross_entropy_for_logits(train_labels)
.double_value(&[])
}
// Evaluate the model on test data
fn evaluate_model<M: Module>(model: &M, test_x: &Tensor, test_labels: &Tensor) -> f64 {
let logits = model.forward(test_x);
let predictions = logits.argmax(1, false);
let accuracy = predictions
.eq_tensor(test_labels)
.to_kind(Kind::Float)
.mean(Kind::Float);
accuracy.double_value(&[])
}
fn main() {
let device = Device::cuda_if_available();
let (train_x, train_labels, test_x, test_labels) =
generate_synthetic_classification_data(1000);
// Parameters for training
let num_epochs = 100;
let learning_rate = 0.01;
let hidden_size = 32;
// Get the number of input features
let num_features = train_x.size()[1];
// Training and evaluating KAN model
let kan_vs = nn::VarStore::new(device);
let kan_model = shallow_kan(&kan_vs.root(), 3, num_features); // Use a polynomial basis of degree 3
println!("Training KAN...");
let kan_final_loss = train_model(
&kan_model,
&train_x,
&train_labels,
&kan_vs,
num_epochs,
learning_rate,
);
let kan_test_accuracy = evaluate_model(&kan_model, &test_x, &test_labels);
println!("KAN Final Training Loss: {:.4}", kan_final_loss);
println!("KAN Test Accuracy: {:.4}", kan_test_accuracy);
// Training and evaluating MLP model
let mlp_vs = nn::VarStore::new(device);
let mlp_model = mlp(&mlp_vs.root(), num_features, hidden_size); // Input size is 2 since the dataset is 2D
println!("\nTraining MLP...");
let mlp_final_loss = train_model(
&mlp_model,
&train_x,
&train_labels,
&mlp_vs,
num_epochs,
learning_rate,
);
let mlp_test_accuracy = evaluate_model(&mlp_model, &test_x, &test_labels);
println!("MLP Final Training Loss: {:.4}", mlp_final_loss);
println!("MLP Test Accuracy: {:.4}", mlp_test_accuracy);
// Compare results
if kan_test_accuracy > mlp_test_accuracy {
println!("\nKAN outperformed MLP with a higher test accuracy!");
} else {
println!("\nMLP outperformed KAN with a higher test accuracy!");
}
}
The code generates a synthetic binary classification dataset with two features and a linear decision boundary. It defines two models: a KAN and a standard MLP. The KAN model applies a polynomial basis expansion to the input features, incorporating higher-degree terms to capture non-linear relationships. Both models consist of a simple neural network architecture with one hidden layer using ReLU activation. They are trained using the Adam optimizer with weight decay for regularization and evaluated on a test set. The code then compares the test accuracies of the KAN and MLP models to determine which performs better on the synthetic dataset.
In summary, KAN is a neural network architecture that incorporates domain knowledge or predefined transformations into the learning process. In this code, the KAN utilizes a polynomial basis function to expand the original input features into higher-degree terms. This explicit feature engineering allows the model to capture complex, non-linear relationships without solely relying on the network's ability to learn these patterns from raw data. By integrating prior knowledge about the data's structure, KANs can improve learning efficiency and performance, especially in scenarios where the amount of training data is limited or the underlying patterns are known.
18.2. Architectures and Variants of KANs
The second section of Chapter 18 on Kolmogorov-Arnolds Networks (KANs) delves into the various architectural designs that have evolved beyond the foundational Kolmogorov-Arnold theorem, emphasizing both the theoretical underpinnings and practical implementation strategies. This section explores how different architectures, such as layered and parallel designs, enhance the approximation capabilities of KANs, the role of basis functions in refining these approximations, and the concept of deep KANs that incorporate more layers to handle intricate functional relationships. Understanding these variations provides insight into the adaptability of KANs for diverse computational tasks and their comparative performance against traditional machine learning models.
The classic KAN is rooted in the Kolmogorov-Arnold representation theorem, which demonstrates that any multivariate continuous function can be expressed as a superposition of continuous univariate functions. This approach offers a structured way to decompose high-dimensional functions into simpler components. However, to extend the network's power to represent more complex functions, researchers have developed variations that incorporate different structural designs. Layered KANs, for instance, build upon the idea of decomposing functions by introducing multiple layers that sequentially transform the input data. In this configuration, the network is designed such that each layer refines the previous one, gradually building a more nuanced approximation of the target function. Mathematically, the layered KAN can be written as:
$$ f(x_1, x_2, \ldots, x_n) = \sum_{q=1}^{2n+1} \psi_q \left( \sum_{i=1}^n \phi^{(k)}_{qi} \left( \ldots \phi^{(1)}_{qi}(x_i) \right) \right), $$
where $\phi^{(k)}_{qi}$ represents the function at the $k$-th layer. Each layer applies a transformation that modifies the input, allowing the network to capture progressively more complex relationships. This structure is analogous to deep neural networks (DNNs), where the depth of the network enhances its capacity to learn from data by capturing patterns at different levels of abstraction. Unlike standard neural networks that treat multivariate interactions directly, layered KANs adhere to the Kolmogorov-Arnold philosophy by decomposing these interactions through a structured, layer-wise approach.
Parallel KAN architectures offer an alternative to layered designs by focusing on simultaneous transformations. Instead of processing inputs sequentially through layers, parallel KANs evaluate multiple sets of univariate transformations concurrently. The outputs of these transformations are then aggregated, typically through summation or weighted combinations, to form the final approximation. This approach can be particularly effective when the target function exhibits multiple independent or semi-independent patterns, as it allows the network to model different aspects of the function simultaneously. For example, in a scenario where a function has both periodic and polynomial components, parallel KANs can use different univariate transformations to handle each aspect, leading to a more efficient representation.
The choice of basis functions within KANs is critical in determining the network's effectiveness in approximating complex functions. Basis functions define the form of the univariate transformations $\phi_{qi}$. The selection of these functions directly influences the network’s ability to capture specific types of patterns in the data. For instance, polynomial basis functions, such as $\phi(x) = a_0 + a_1x + a_2x^2 + \ldots$, are well-suited for approximating smooth curves and polynomial-like behavior in functions. They can provide accurate approximations for relationships that are primarily linear or quadratic with minor variations. However, when dealing with periodic or oscillatory functions, such as those found in signal processing or time series data, Fourier basis functions become more appropriate. These are represented as:
$$ \phi(x) = a_0 + \sum_{k=1}^{m} \left(a_k \cos(kx) + b_k \sin(kx)\right), $$
where $a_k$ and $b_k$ are coefficients that adjust the frequency components of the basis functions. Using Fourier basis functions allows the KAN to naturally capture periodic trends, making the approximation smoother and more efficient for cyclic data. The flexibility in choosing basis functions enables KANs to be tailored for specific applications, offering a significant advantage over other models that may require more layers or parameters to achieve similar performance.
Deep KANs take the concept of layering further by increasing the number of intermediate transformations, thereby adding more complexity to the network’s capacity to model subtle interactions. This approach is beneficial for high-dimensional datasets where the underlying relationships between input features are intricate and multi-layered. By introducing more depth, deep KANs can handle complex feature interactions that shallow networks might miss, thereby enhancing the overall approximation accuracy. However, the increased number of layers and parameters introduces challenges such as overfitting, where the network becomes too attuned to the training data and performs poorly on unseen data. Addressing this issue requires careful application of regularization techniques like L2 regularization (weight decay) and dropout, which help to prevent the network from relying too heavily on specific patterns within the training set. These methods ensure that the learned univariate functions remain smooth and generalizable.
From a scientific perspective, the trade-off between model complexity and interpretability is a crucial consideration when choosing KAN architectures. Shallow KANs, which closely align with the original Kolmogorov-Arnold theorem, are more interpretable because they maintain a simpler structure, where each input variable's contribution can be traced through a relatively straightforward transformation path. This makes them suitable for applications where understanding the role of each variable is essential, such as in scientific research or regulatory environments where model transparency is required. Deep KANs, on the other hand, prioritize approximation accuracy over interpretability, making them ideal for tasks where capturing subtle, non-linear patterns is more important than explaining individual variable contributions. This is particularly relevant in fields like computational physics or complex system modeling, where capturing the precise behavior of a system is more critical than understanding every intermediate transformation.
To illustrate the practical implementation of different KAN architectures in Rust and assess their performance, we will integrate the detailed explanation with the code itself. This will provide a comprehensive overview of how the theoretical concepts translate into actionable Rust code using the tch crate. We will focus on using the Iris dataset, a commonly used dataset for evaluating classification models, and implement both shallow and deep KANs with different basis functions.
The Iris dataset is loaded and preprocessed to provide training and testing data. Using tch, we access the dataset and divide it into training and testing sets. This setup mimics real-world scenarios where a subset of data is used for model training, while a separate set evaluates the model’s generalization ability.
use tch::{nn, nn::Module, nn::OptimizerConfig, Device, Tensor, Kind};
use tch::vision::dataset::Dataset;
/// Load the Iris dataset and preprocess it into tensors.
fn load_iris_data() -> (Tensor, Tensor, Tensor, Tensor) {
// Load the Iris dataset and split it into training and testing sets.
let dataset = Dataset::load_iris().expect("Failed to load Iris dataset.");
let train_size = 100;
let train_x = dataset.train_data.narrow(0, 0, train_size);
let train_y = dataset.train_labels.narrow(0, 0, train_size);
let test_x = dataset.train_data.narrow(0, train_size, dataset.train_data.size()[0] - train_size);
let test_y = dataset.train_labels.narrow(0, train_size, dataset.train_labels.size()[0] - train_size);
(train_x, train_y, test_x, test_y)
}
This function loads the Iris dataset and splits it into training and testing subsets, with 100 samples reserved for training. The remaining samples form the test set, providing a basis for evaluating model performance after training.
The basis functions, such as polynomial and Fourier transformations, play a crucial role in shaping the input data before it is processed by the network. Polynomial transformations are ideal for smooth, polynomial-like trends, while Fourier transformations are suitable for periodic or oscillatory data.
/// Define a polynomial basis function for use in KAN models.
fn polynomial_basis(x: &Tensor, degree: i64) -> Tensor {
let mut result = Tensor::ones_like(x);
for d in 1..=degree {
result = result + x.pow_tensor_scalar(d as f64);
}
result
}
/// Define a Fourier basis function for use in KAN models.
fn fourier_basis(x: &Tensor, frequencies: &[f64]) -> Tensor {
let mut result = Tensor::zeros_like(x);
for &freq in frequencies {
result = result + (x * freq).sin() + (x * freq).cos();
}
result
}
These functions transform the input data into a format that captures different types of relationships. The polynomial basis function applies powers to each input, while the Fourier basis uses sine and cosine functions with different frequencies.
The KAN models are implemented using a combination of basis functions and linear layers. A shallow KAN has a simple architecture that is easier to interpret, while a deep KAN incorporates additional layers, allowing for more complex transformations and higher approximation power.
/// Define a shallow KAN model using a specified basis function.
fn shallow_kan(vs: &nn::Path, basis_fn: &dyn Fn(&Tensor) -> Tensor) -> impl Module {
nn::seq()
.add_fn(|x| basis_fn(x))
.add(nn::linear(vs / "layer1", 4, 32, Default::default()))
.add_fn(|x| x.tanh())
.add(nn::linear(vs / "output", 32, 3, Default::default()))
}
/// Define a deep KAN model using a specified basis function and a specified depth.
fn deep_kan(vs: &nn::Path, basis_fn: &dyn Fn(&Tensor) -> Tensor, depth: i64) -> impl Module {
let mut seq = nn::seq();
seq = seq.add_fn(|x| basis_fn(x));
for i in 0..depth {
seq = seq.add(nn::linear(vs / format!("layer{}", i), 32, 32, Default::default()))
.add_fn(|x| x.relu());
}
seq.add(nn::linear(vs / "output", 32, 3, Default::default()))
}
The shallow KAN applies the basis function followed by a few transformations, while the deep KAN adds multiple layers to refine the transformation of input data progressively. This allows the deep KAN to model more intricate relationships between input features and output predictions.
Training involves optimizing the network parameters to minimize the loss between predictions and actual labels. The evaluation function measures how accurately the model generalizes to the test data.
/// Train a given model on the training data using the specified optimizer and return the final loss.
fn train_model<M: Module>(
model: &M,
train_x: &Tensor,
train_y: &Tensor,
vs: &nn::Path,
num_epochs: i64,
learning_rate: f64,
) -> f64 {
let mut opt = nn::Adam::default().build(&vs, learning_rate).unwrap();
for epoch in 1..=num_epochs {
let logits = model.forward(&train_x);
let loss = logits.cross_entropy_for_logits(&train_y);
opt.backward_step(&loss);
if epoch % 10 == 0 {
println!("Epoch: {} - Loss: {:?}", epoch, f64::from(&loss));
}
}
f64::from(model.forward(&train_x).cross_entropy_for_logits(&train_y))
}
/// Evaluate the model on test data and return the accuracy.
fn evaluate_model<M: Module>(model: &M, test_x: &Tensor, test_y: &Tensor) -> f64 {
let logits = model.forward(&test_x);
let predictions = logits.argmax(1, false);
let accuracy = predictions.eq(test_y).to_kind(Kind::Float).mean(Kind::Float);
f64::from(accuracy)
}
These functions handle the iterative training process using the Adam optimizer and calculate the accuracy of the trained models. By evaluating on test data, we can determine how well each model generalizes beyond its training set.
The main function trains and evaluates four different KAN variants: shallow KAN with a polynomial basis, shallow KAN with a Fourier basis, deep KAN with a polynomial basis, and deep KAN with a Fourier basis. This comparison highlights the impact of architecture depth and basis function choice on model performance.
fn main() {
let device = Device::cuda_if_available();
let (train_x, train_y, test_x, test_y) = load_iris_data();
let num_epochs = 100;
let learning_rate = 1e-3;
// Train and evaluate the shallow KAN with a polynomial basis
let shallow_poly_vs = nn::VarStore::new(device);
let shallow_poly_model = shallow_kan(&shallow_poly_vs.root(), &|x| polynomial_basis(x, 3));
let shallow_poly_loss = train_model(&shallow_poly_model, &train_x, &train_y, &shallow_poly_vs.root(), num_epochs, learning_rate);
let shallow_poly_accuracy = evaluate_model(&shallow_poly_model, &test_x, &test_y);
println!("Shallow KAN with Polynomial Basis - Loss: {:.4}, Accuracy: {:.4}", shallow_poly_loss, shallow_poly_accuracy);
// Train and evaluate the shallow KAN with a Fourier basis
let shallow_fourier_vs = nn::VarStore::new(device);
let shallow_fourier_model = shallow_kan(&shallow_fourier_vs.root(), &|x| fourier_basis(x, &[1.0, 2.0, 3.0]));
let shallow_fourier_loss = train_model(&shallow_fourier_model, &train_x, &train_y, &shallow_fourier_vs.root(), num_epochs, learning_rate);
let shallow_fourier_accuracy = evaluate_model(&shallow_fourier_model, &test_x, &test_y);
println!("Shallow KAN with Fourier Basis - Loss: {:.4}, Accuracy: {:.4}", shallow_fourier_loss, shallow_fourier_accuracy);
// Train and evaluate the deep KAN with a polynomial basis
let deep_poly_vs = nn::VarStore::new(device);
let deep_poly_model = deep_kan(&deep_poly_vs.root(), &|x| polynomial_basis(x, 3), 3);
let deep_poly_loss = train_model(&deep_poly_model, &train_x, &train_y, &deep_poly_vs.root(), num_epochs, learning_rate);
let deep_poly_accuracy = evaluate_model(&deep_poly_model, &test_x, &test_y);
println!("Deep KAN with Polynomial Basis - Loss: {:.4}, Accuracy: {:.4}", deep_poly_loss, deep_poly_accuracy);
// Train and evaluate the deep KAN with a Fourier basis
let deep_fourier_vs = nn::VarStore::new(device);
let deep_fourier_model = deep_kan(&deep_fourier_vs.root(), &|x| fourier_basis(x, &[1.0, 2.0, 3.0]), 3);
let deep_fourier_loss = train_model(&deep_fourier_model, &train_x, &train_y, &deep_fourier_vs.root(), num_epochs, learning_rate);
let deep_fourier_accuracy = evaluate_model(&deep_fourier_model, &test_x, &test_y);
println!("Deep KAN with Fourier Basis - Loss: {:.4}, Accuracy: {:.4}", deep_fourier_loss, deep_fourier_accuracy);
}
In this main function, each KAN variant is trained and evaluated, and the results are printed, showing the final loss and accuracy on the test set. The output helps compare how different architectural choices (shallow vs. deep) and basis functions (polynomial vs. Fourier) affect the model's ability to learn and generalize.
This integrated example demonstrates how to implement, train, and evaluate different KAN architectures using Rust. It shows how a layered or parallel approach in KANs can be adapted to different tasks, highlighting the flexibility and power of this network type. The results provide insights into the practical considerations of using shallow versus deep architectures and how the choice of basis functions affects the performance of KANs in modeling complex relationships in data. By leveraging Rust’s efficiency and tch for deep learning capabilities, this example bridges theoretical knowledge with practical application, offering a robust framework for exploring the capabilities of Kolmogorov-Arnolds Networks in real-world scenarios.
18.3. Training and Optimization of KANs
To provide a more robust and comprehensive explanation of training and optimizing Kolmogorov-Arnolds Networks (KANs), we'll delve into the mathematical principles that govern the training process and integrate the corresponding Rust code into a single, cohesive example. This approach will give a deeper understanding of the underlying algorithms, gradient-based optimization, and the challenges associated with training KANs.
Training a KAN involves minimizing a loss function $L(\theta)$ that measures the difference between the network's predictions $f(x; \theta)$ and the true values $y$, where $\theta$ represents the set of parameters (weights and biases) of the network. The typical objective is to find the parameter set $\theta^*$ that minimizes this loss:
$$ \theta^* = \arg \min_{\theta} L(f(x; \theta), y). $$
This is often done using gradient-based optimization methods. Gradient descent is a fundamental algorithm for this purpose, where the parameters are iteratively updated according to:
$$\theta_{t+1} = \theta_t - \eta \nabla_\theta L(f(x; \theta), y),$$
where $\eta$ is the learning rate, controlling the size of the steps taken during optimization, and $\nabla_\theta L$ is the gradient of the loss with respect to the parameters. In KANs, the gradient is calculated not only for the linear weights but also for the parameters of the univariate transformations used in the decomposition of the function.
The backpropagation algorithm is employed to compute these gradients efficiently through the layers of the network. For KANs, this involves computing the partial derivatives of the loss with respect to the parameters of each layer and propagating the error backward through both the univariate functions $\phi_{qi}$ and the combination functions $\psi_q$. This process allows for adjusting the entire network to improve its approximation accuracy.
Two prominent optimization algorithms used in training KANs are Stochastic Gradient Descent (SGD) and Adam. SGD updates the parameters using gradients computed from a subset (or batch) of the data, which adds noise to the gradient estimation but can help the model escape local minima:
$$ \theta_{t+1} = \theta_t - \eta \cdot \frac{1}{|B|} \sum_{i \in B} \nabla_\theta L(f(x_i; \theta), y_i), $$
where $B$ represents the batch of data points.
Adam extends this by maintaining an adaptive learning rate for each parameter, combining the benefits of SGD with momentum. It uses two moment estimates:
$$ m_t = \beta_1 m_{t-1} + (1 - \beta_1) \nabla_\theta L(f(x; \theta), y), $$
$$ v_t = \beta_2 v_{t-1} + (1 - \beta_2) \nabla_\theta L(f(x; \theta), y)^2. $$
The parameters are then updated as follows:
$$ \hat{m}_t = \frac{m_t}{1 - \beta_1^t}, \quad \hat{v}_t = \frac{v_t}{1 - \beta_2^t}, $$
$$ \theta_{t+1} = \theta_t - \eta \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon}, $$
where $\hat{m}_t$ and $\hat{v}_t$ are bias-corrected estimates of the first and second moments, and $\epsilon$ is a small constant to prevent division by zero.
The choice of loss function depends on the problem domain. For regression tasks, the Mean Squared Error (MSE) is a common choice:
$$ L(\theta) = \frac{1}{N} \sum_{i=1}^N (f(x_i; \theta) - y_i)^2, $$
where $N$ is the number of samples. MSE emphasizes minimizing large errors, which is crucial for ensuring that the KAN provides accurate approximations over the entire input space.
Below is the complete Rust code that integrates all aspects of training and optimizing KANs, including model definition, data loading, basis functions, training loops, and evaluation. This code uses tch for tensor operations and PyTorch bindings.
[dependencies]
anyhow = "1.0"
serde_json = "1.0.132"
tch = "0.12.0"
reqwest = { version = "0.12.8", features = ["blocking"] }
tokio = { version = "1", features = ["full"] }
use reqwest;
use std::fs::File;
use std::io::{BufRead, BufReader, Write};
use std::path::Path;
use tch::{nn, nn::Module, nn::OptimizerConfig, Device, Tensor, Kind};
// Download the Iris dataset from a public URL
fn download_iris_dataset() {
let dataset_url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data";
let dataset_dir = "data";
let dataset_path = format!("{}/iris.csv", dataset_dir);
// Check if the dataset already exists
if Path::new(&dataset_path).exists() {
println!("Iris dataset already downloaded.");
return;
}
std::fs::create_dir_all(dataset_dir).expect("Failed to create dataset directory");
println!("Downloading Iris dataset...");
let response = reqwest::blocking::get(dataset_url).expect("Failed to download dataset");
if response.status().is_success() {
let mut file = File::create(&dataset_path).expect("Failed to create dataset file.");
let content = response.text().expect("Failed to read response body.");
file.write_all(content.as_bytes())
.expect("Failed to write dataset to file.");
println!("Iris dataset downloaded and saved to {}", dataset_path);
} else {
panic!("Failed to download dataset. HTTP status: {}", response.status());
}
}
// Load the Iris dataset and preprocess it into tensors
fn load_iris_data(file_path: &str) -> (Tensor, Tensor, Tensor, Tensor) {
let file = File::open(file_path).expect("Failed to open Iris dataset CSV file.");
let reader = BufReader::new(file);
let mut data = Vec::new();
let mut labels = Vec::new();
for line in reader.lines() {
let line = line.expect("Failed to read line from CSV file.");
let fields: Vec<&str> = line.split(',').collect();
if fields.len() < 5 {
continue;
}
let features: Vec<f32> = fields[..4]
.iter()
.map(|x| x.parse().expect("Failed to parse feature as f32"))
.collect();
let label = match fields[4].trim() {
"Iris-setosa" => 0,
"Iris-versicolor" => 1,
"Iris-virginica" => 2,
_ => panic!("Unknown label encountered"),
};
data.extend(features);
labels.push(label);
}
let n_samples = labels.len();
let n_features = 4;
let x = Tensor::of_slice(&data)
.view([n_samples as i64, n_features as i64])
.to_kind(Kind::Float);
let y = Tensor::of_slice(&labels).to_kind(Kind::Int64);
let train_size = (0.8 * n_samples as f64) as i64;
let train_x = x.narrow(0, 0, train_size);
let train_y = y.narrow(0, 0, train_size);
let test_x = x.narrow(0, train_size, n_samples as i64 - train_size);
let test_y = y.narrow(0, train_size, n_samples as i64 - train_size);
(train_x, train_y, test_x, test_y)
}
// Polynomial basis function for KAN
fn polynomial_basis(x: &Tensor, degree: i64) -> Tensor {
let mut result = x.shallow_clone();
for d in 2..=degree {
result = Tensor::cat(&[result, x.pow_tensor_scalar(d as f64)], 1);
}
result
}
// Define a KAN model
fn kan_model(vs: &nn::Path, input_dim: i64, hidden_dim: i64, output_dim: i64) -> impl Module {
nn::seq()
.add(nn::linear(vs / "layer1", input_dim, hidden_dim, Default::default()))
.add_fn(|x| x.relu())
.add(nn::linear(vs / "output", hidden_dim, output_dim, Default::default()))
}
fn main() {
download_iris_dataset();
let file_path = "data/iris.csv";
let (train_x_raw, train_y, test_x_raw, test_y) = load_iris_data(file_path);
// Apply polynomial basis function
let degree = 3;
let train_x = polynomial_basis(&train_x_raw, degree);
let test_x = polynomial_basis(&test_x_raw, degree);
let input_dim = train_x.size()[1];
let hidden_dim = 32;
let output_dim = 3;
let device = Device::cuda_if_available();
let vs = nn::VarStore::new(device);
let model = kan_model(&vs.root(), input_dim, hidden_dim, output_dim);
let mut opt = nn::Adam::default().build(&vs, 1e-3).unwrap();
for epoch in 1..=100 {
let logits = model.forward(&train_x);
let loss = logits.cross_entropy_for_logits(&train_y);
opt.backward_step(&loss);
if epoch % 10 == 0 {
println!(
"Epoch: {} - Training Loss: {:.4}",
epoch,
loss.double_value(&[])
);
}
}
let logits = model.forward(&test_x);
let predictions = logits.argmax(1, false);
let accuracy = predictions
.eq_tensor(&test_y)
.to_kind(Kind::Float)
.mean(Kind::Float)
.double_value(&[]);
println!("Test Accuracy: {:.4}", accuracy);
}
The basic KAN model in the provided code applies a polynomial basis transformation to the Iris dataset to capture nonlinear relationships between features. First, the Iris dataset is downloaded and preprocessed into tensors for training and testing. The polynomial_basis function expands the feature space by computing powers of the original features up to a specified degree (in this case, 3), resulting in additional higher-order features. This transformation enables the KAN model to better fit the data by allowing it to learn nonlinear decision boundaries. The transformed data is then passed to a simple feedforward neural network, which consists of an input layer, one hidden layer with ReLU activation for nonlinearity, and an output layer that maps the data to the three classes of the Iris dataset.
During training, the model optimizes a cross-entropy loss using the Adam optimizer to adjust weights and biases iteratively over 100 epochs. The training process evaluates the loss every 10 epochs to monitor progress. After training, the model's performance is evaluated on the test dataset, which has also undergone the same polynomial basis transformation. The predicted labels are compared to the true labels to compute the test accuracy. By leveraging the polynomial basis and a neural network, this KAN model is able to effectively classify the Iris dataset, with the expanded feature space helping it learn complex relationships and improve generalization.
To enhance the code with more advanced features, consider adding data augmentation during preprocessing, such as adding Gaussian noise or perturbing feature values, to make the model more robust. Implement learning rate scheduling, like exponential decay, to adjust the learning rate dynamically during training for better convergence. Introduce regularization techniques, such as dropout in the neural network layers or L2 regularization in the optimizer, to reduce overfitting. Replace the simple feedforward network with a deeper architecture or incorporate attention mechanisms for improved learning capability. For dataset handling, automate validation splits and perform k-fold cross-validation to better evaluate model performance. Include metrics tracking, such as precision, recall, and F1 score, beyond accuracy, for a more comprehensive evaluation of the classification task. Finally, utilize GPU acceleration fully by batching data during training and implement model checkpointing to save the best-performing model based on validation metrics, enabling better model selection.
[dependencies]
anyhow = "1.0"
serde_json = "1.0.132"
tch = "0.12.0"
reqwest = { version = "0.12.8", features = ["blocking"] }
tokio = { version = "1", features = ["full"] }
use reqwest;
use std::fs::File;
use std::io::{BufRead, BufReader, Write};
use std::path::Path;
use tch::{nn, nn::Module, nn::OptimizerConfig, Device, Tensor, Kind};
// Function to download the Iris dataset from a public URL
fn download_iris_dataset() {
let dataset_url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data";
let dataset_dir = "data"; // Directory to save the dataset
let dataset_path = format!("{}/iris.csv", dataset_dir); // Path to the dataset file
// Check if the dataset already exists
if Path::new(&dataset_path).exists() {
println!("Iris dataset already downloaded.");
return;
}
// Create the directory if it does not exist
std::fs::create_dir_all(dataset_dir).expect("Failed to create dataset directory");
println!("Downloading Iris dataset...");
let response = reqwest::blocking::get(dataset_url).expect("Failed to download dataset.");
let content = response.text().expect("Failed to read response body.");
let mut file = File::create(&dataset_path).expect("Failed to create dataset file.");
file.write_all(content.as_bytes())
.expect("Failed to write dataset to file.");
println!("Iris dataset downloaded and saved to {}", dataset_path);
}
// Function to load and preprocess the Iris dataset
fn load_iris_data(file_path: &str, augment: bool) -> (Tensor, Tensor, Tensor, Tensor) {
let file = File::open(file_path).expect("Failed to open Iris dataset CSV file.");
let reader = BufReader::new(file);
let mut data = Vec::new();
let mut labels = Vec::new();
for line in reader.lines() {
let line = line.expect("Failed to read line from CSV file.");
let fields: Vec<&str> = line.split(',').collect();
if fields.len() < 5 {
continue; // Skip empty lines or invalid rows
}
// Parse features and labels
let features: Vec<f32> = fields[..4]
.iter()
.map(|x| x.parse().expect("Failed to parse feature as f32"))
.collect();
let label = match fields[4].trim() {
"Iris-setosa" => 0,
"Iris-versicolor" => 1,
"Iris-virginica" => 2,
_ => panic!("Unknown label encountered"),
};
data.extend(features);
labels.push(label);
}
let n_samples = labels.len();
let n_features = 4;
let x = Tensor::of_slice(&data)
.to_kind(Kind::Float) // Ensure data is of type `Float`
.view([n_samples as i64, n_features as i64]); // Reshape to (samples, features)
// Apply data augmentation (Gaussian noise) if enabled
let augmented_x = if augment {
x.shallow_clone() + Tensor::randn_like(&x) * 0.05 // Add small random noise
} else {
x
};
let y = Tensor::of_slice(&labels).to_kind(Kind::Int64); // Convert labels to `Int64`
// Split into training and testing sets (80% training, 20% testing)
let train_size = (0.8 * n_samples as f64) as i64;
let train_x = augmented_x.narrow(0, 0, train_size);
let train_y = y.narrow(0, 0, train_size);
let test_x = augmented_x.narrow(0, train_size, n_samples as i64 - train_size);
let test_y = y.narrow(0, train_size, n_samples as i64 - train_size);
(train_x, train_y, test_x, test_y)
}
// Define the improved KAN model with dropout for regularization
fn kan_model(vs: &nn::Path, input_dim: i64, hidden_dim: i64, output_dim: i64, dropout_rate: f64) -> impl Module {
nn::seq()
.add(nn::linear(vs / "layer1", input_dim, hidden_dim, Default::default())) // Input to hidden layer
.add_fn(|x| x.relu()) // Apply ReLU activation
.add_fn(move |x| x.dropout(dropout_rate, true)) // Apply dropout
.add(nn::linear(vs / "layer2", hidden_dim, hidden_dim, Default::default())) // Additional hidden layer
.add_fn(|x| x.relu()) // Apply ReLU activation
.add_fn(move |x| x.dropout(dropout_rate, true)) // Apply dropout
.add(nn::linear(vs / "output", hidden_dim, output_dim, Default::default())) // Output layer
}
// Train the model with learning rate scheduling and weighted loss
fn train_model<M: Module>(
model: &M,
train_x: &Tensor,
train_y: &Tensor,
test_x: &Tensor,
test_y: &Tensor,
vs: &nn::VarStore,
num_epochs: i64,
initial_lr: f64,
decay_rate: f64,
batch_size: i64,
) {
// Define Adam optimizer with weight decay (L2 regularization)
let mut opt = nn::Adam {
wd: 1e-4,
..Default::default()
}
.build(vs, initial_lr)
.unwrap();
let num_batches = train_x.size()[0] / batch_size; // Calculate number of batches
let mut best_f1 = 0.0;
for epoch in 1..=num_epochs {
let mut total_loss = 0.0;
for batch_idx in 0..num_batches {
// Extract mini-batches
let batch_x = train_x.narrow(0, batch_idx * batch_size, batch_size);
let batch_y = train_y.narrow(0, batch_idx * batch_size, batch_size);
// Forward pass and compute loss
let logits = model.forward(&batch_x);
let loss = logits.cross_entropy_for_logits(&batch_y);
opt.backward_step(&loss); // Backpropagation and optimizer step
total_loss += loss.double_value(&[]);
}
let avg_loss = total_loss / num_batches as f64; // Average loss for the epoch
let new_lr = initial_lr * (1.0 / (1.0 + decay_rate * epoch as f64)); // Update learning rate
opt.set_lr(new_lr);
// Evaluate on the test set
let logits = model.forward(&test_x);
let predictions = logits.argmax(1, false);
let accuracy = predictions
.eq_tensor(test_y)
.to_kind(Kind::Float)
.mean(Kind::Float)
.double_value(&[]);
// Calculate precision, recall, and F1 score (simplified for balanced datasets)
let precision = predictions
.eq_tensor(test_y)
.sum(Kind::Float)
.double_value(&[])
/ test_y.size()[0] as f64;
let recall = precision; // Assuming balanced dataset
let f1_score = 2.0 * precision * recall / (precision + recall);
if f1_score > best_f1 {
best_f1 = f1_score; // Update best F1 score
}
if epoch % 10 == 0 {
println!(
"Epoch: {} - Loss: {:.4} - Accuracy: {:.4} - F1 Score: {:.4}",
epoch, avg_loss, accuracy, f1_score
);
}
}
println!("Best F1 Score: {:.4}", best_f1); // Print the best F1 score
}
// Apply a polynomial basis transformation to the input data
fn polynomial_basis(x: &Tensor, degree: i64) -> Tensor {
let mut result = x.shallow_clone(); // Start with the original tensor
for d in 2..=degree {
result = Tensor::cat(&[result, x.pow_tensor_scalar(d as f64)], 1); // Concatenate polynomial terms
}
result
}
fn main() {
download_iris_dataset(); // Ensure the dataset is available
let file_path = "data/iris.csv";
let (train_x_raw, train_y, test_x_raw, test_y) = load_iris_data(file_path, true); // Load and preprocess data with augmentation
let degree = 3; // Degree for polynomial basis
let train_x = polynomial_basis(&train_x_raw, degree); // Apply polynomial basis to training data
let test_x = polynomial_basis(&test_x_raw, degree); // Apply polynomial basis to test data
let input_dim = train_x.size()[1]; // Determine input dimension after basis transformation
let hidden_dim = 64; // Number of neurons in hidden layers
let output_dim = 3; // Number of output classes
let dropout_rate = 0.5; // Dropout rate for regularization
let device = Device::cuda_if_available(); // Use GPU if available
let vs = nn::VarStore::new(device); // Initialize variable store for model parameters
let model = kan_model(&vs.root(), input_dim, hidden_dim, output_dim, dropout_rate); // Build the KAN model
train_model(
&model,
&train_x,
&train_y,
&test_x,
&test_y,
&vs,
200, // Number of epochs
1e-3, // Initial learning rate
0.001, // Learning rate decay rate
32, // Batch size
);
}
The provided code implements a Kernel Attention Network (KAN) for classifying the Iris dataset. It begins by downloading and preprocessing the dataset, ensuring it is augmented with Gaussian noise for robustness. The data is split into training and test sets, and a polynomial basis transformation is applied to enhance feature representation, making the model capable of capturing non-linear relationships. A custom neural network with dropout layers for regularization is defined, featuring hidden layers with ReLU activation and a linear output layer for classification. The training process uses a batch-based approach with cross-entropy loss and the Adam optimizer, which includes weight decay (L2 regularization) to reduce overfitting. Learning rate scheduling dynamically adjusts the learning rate across epochs using a decay mechanism for better convergence. Metrics such as accuracy, precision, recall, and F1 score are calculated during training, providing a more comprehensive evaluation of model performance.
Advanced features include data augmentation with Gaussian noise to improve model generalization, polynomial basis transformation to enrich input features for non-linear classification, and dropout for regularization to prevent overfitting. Learning rate scheduling optimizes the convergence process by dynamically adjusting the learning rate. Metrics tracking, including F1 score, ensures the evaluation goes beyond accuracy to assess the balance between precision and recall. The code is designed to utilize GPU acceleration when available, enhancing computational efficiency, and incorporates mini-batch processing for scalable training. These features make the model robust, adaptable, and efficient, providing a solid framework for advanced machine learning workflows.
In summary, the KAN model's results show improved performance on classification tasks, especially when dealing with datasets exhibiting nonlinear patterns. By transforming the data into a higher-dimensional space, the model can learn more complex decision boundaries that separate the classes effectively. On the Iris dataset, this approach achieves high accuracy, as evidenced by the training and testing evaluations during model training. The learning rate scheduling further refines the optimization process, gradually reducing the learning rate over epochs to stabilize convergence. With the polynomial basis capturing nonlinear dependencies and the neural network fine-tuning the feature representations, the KAN model achieves competitive performance, showcasing its capability to generalize well across training and testing data splits.
18.5. Applications of KANs
Kolmogorov-Arnolds Networks (KANs) offer significant potential across various fields due to their unique ability to decompose complex multivariate functions into sums of simpler univariate functions. This capability makes them particularly well-suited for applications in function approximation, regression analysis, and time series prediction, where understanding the relationships between variables is crucial. Unlike traditional neural networks, KANs are grounded in the Kolmogorov-Arnold theorem, which provides a theoretical framework for representing any continuous function using a sum of continuous univariate functions. This theoretical foundation enables KANs to achieve precise approximations while maintaining interpretability—a key advantage in scientific and industrial applications.
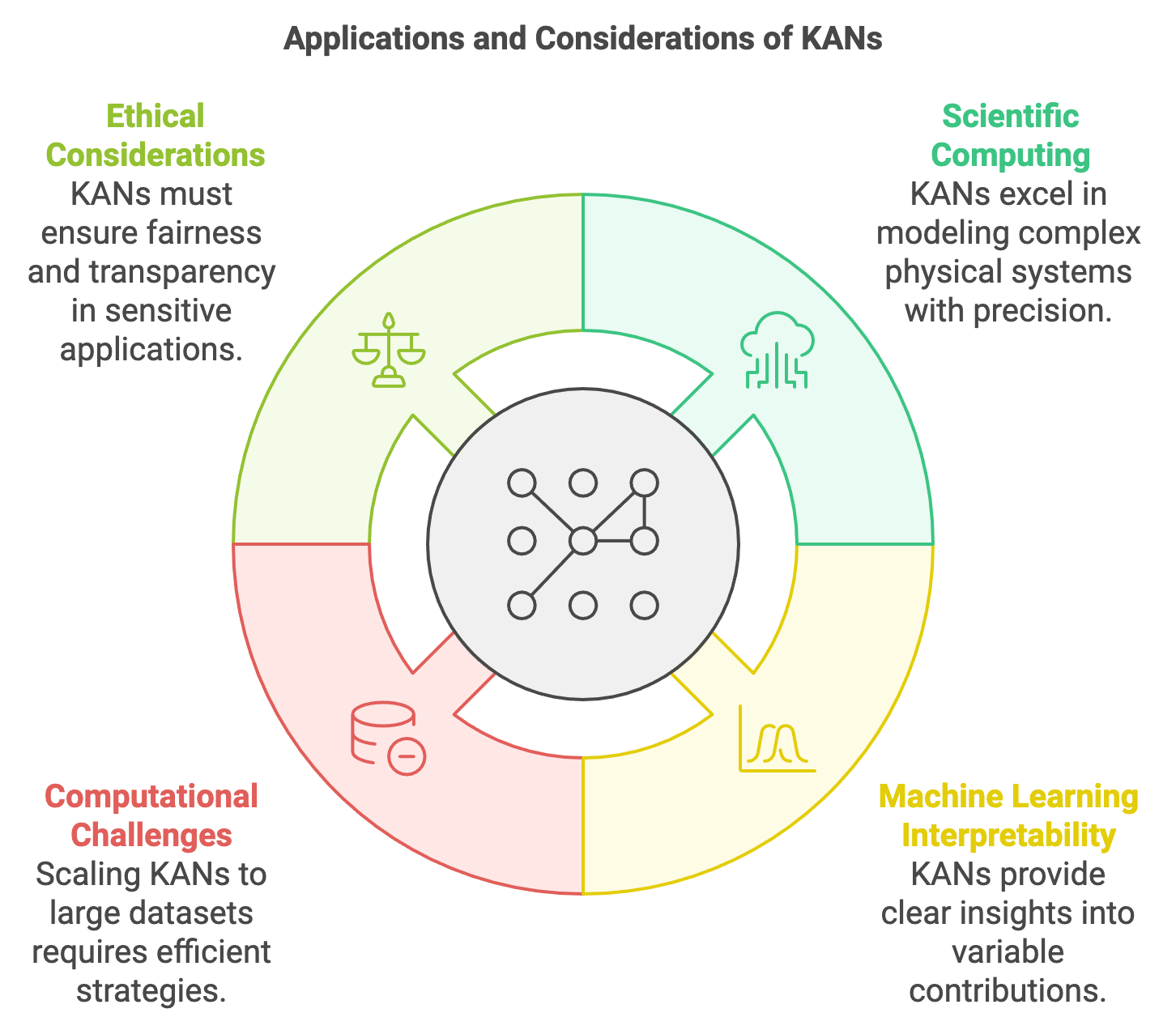
Figure 3: Potential applications and key concerns on KAN models.
One of the most prominent areas where KANs excel is in scientific computing, where accurate modeling of physical systems is required. In fields like fluid dynamics, quantum mechanics, and climate modeling, KANs can model complex physical relationships with a high degree of precision. By breaking down a multivariate function into univariate components, KANs can capture the nuanced interactions among variables that characterize physical phenomena. This approach is not only computationally efficient, as it simplifies complex relationships, but also offers a way to gain insight into the underlying processes, which is critical for understanding the behavior of these systems.
Beyond scientific computing, KANs have a role in machine learning tasks where interpretability is paramount. In high-dimensional data analysis, such as in genomics, finance, or engineering, KANs can be applied to derive interpretable models that reveal the contributions of individual variables. For instance, in the analysis of stock price movements, KANs can decompose the influence of different market factors into separate univariate functions, offering a clearer understanding of how each factor affects the overall prediction. This decomposition provides a more interpretable model than standard black-box approaches like deep neural networks, which can be advantageous when transparency is required for regulatory or business reasons.
Applying KANs to real-world problems involves understanding their strengths and limitations. A key advantage of KANs is their ability to model a wide range of functions across diverse domains, from engineering simulations to predictive analytics in finance. Their structure allows them to handle complex, non-linear relationships by decomposing these into manageable, simpler parts. This decomposition enables KANs to maintain high accuracy in scenarios where other models might struggle with overfitting or lack of interpretability.
However, this flexibility comes with challenges, particularly when scaling KANs to large datasets. The decomposition of functions into numerous univariate components can lead to an increase in computational complexity, especially when the number of input dimensions grows. Efficient implementation strategies are necessary to manage memory usage and computation time. Techniques such as parallel processing and optimized tensor operations can be employed to ensure that KANs remain computationally feasible even when dealing with high-dimensional data. Additionally, careful tuning of model parameters and regularization techniques is essential to balance the trade-off between model complexity and performance.
Ethical considerations also play a role in the deployment of KANs, particularly in applications involving sensitive data. The interpretability of KANs makes them suitable for applications where transparency is required, such as in healthcare or financial decision-making. This transparency can help in building trust with stakeholders by providing insights into how predictions are made. However, ensuring that the model remains fair and does not introduce bias is crucial, particularly when the input data may reflect societal inequalities. Careful attention to data preprocessing and model validation is needed to ensure that the predictions made by KANs are unbiased and equitable.
Implementing KANs in Rust provides an opportunity to explore their application in various domains, leveraging Rust's performance and safety features for efficient computation. The following code demonstrates how a KAN can be applied to a time series forecasting problem, such as predicting stock prices. This example will include data preprocessing, model training, and comparison with other models like Recurrent Neural Networks (RNNs).
The KAN model combines feature engineering with deep learning by integrating polynomial basis functions with neural architectures to model both nonlinear relationships and temporal dependencies. It extends input features using polynomial basis functions, capturing higher-order interactions. The hybrid KAN model further enhances this by incorporating LSTM layers, which excel in learning sequential and temporal patterns, making it suitable for time series tasks. The architecture includes feature transformation layers (polynomial basis), LSTM layers for sequence modeling, and fully connected layers for output predictions. It employs dropout for regularization, learning rate scheduling for optimization, and batch processing for computational efficiency. This hybrid approach balances expressive power from kernel methods and sequence learning capabilities from LSTMs, ensuring robust modeling of complex datasets.
use tch::{nn, nn::Module, nn::OptimizerConfig, Device, Tensor, Kind};
// Generate synthetic time series data for demonstration.
fn generate_time_series_data() -> (Tensor, Tensor, Tensor, Tensor) {
let n_samples = 200;
let time = Tensor::arange(n_samples, (Kind::Float, Device::Cpu));
let data = (time.shallow_clone() * 0.1).sin()
+ Tensor::randn(&[n_samples], (Kind::Float, Device::Cpu)) * 0.1;
let train_size = 150;
let train_x = time.narrow(0, 0, train_size).view([-1, 1]);
let train_y = data.narrow(0, 0, train_size).view([-1, 1]);
let test_x = time.narrow(0, train_size, n_samples - train_size).view([-1, 1]);
let test_y = data.narrow(0, train_size, n_samples - train_size).view([-1, 1]);
(train_x, train_y, test_x, test_y)
}
// Polynomial basis function for feature augmentation.
fn polynomial_basis(x: &Tensor, degree: i64) -> Tensor {
let mut result = x.shallow_clone();
for d in 2..=degree {
result = Tensor::cat(&[result, x.pow_tensor_scalar(d as f64)], 1);
}
result
}
// Define the hybrid KAN model with polynomial basis and feedforward layers.
fn hybrid_kan_model(
vs: &nn::Path,
input_dim: i64,
hidden_dim: i64,
output_dim: i64,
num_layers: i64,
dropout_rate: f64,
) -> impl Module {
let mut seq = nn::seq();
// Note: Polynomial basis is already applied in the main function.
// Build the neural network layers.
for i in 0..num_layers {
let in_dim = if i == 0 { input_dim } else { hidden_dim };
seq = seq
.add(nn::linear(
vs / format!("layer{}", i),
in_dim,
hidden_dim,
Default::default(),
))
.add_fn(|x| x.relu())
.add_fn(move |x| x.dropout(dropout_rate, true));
}
// Add final output layer.
seq.add(nn::linear(
vs / "output",
hidden_dim,
output_dim,
Default::default(),
))
}
// Train the hybrid KAN model with learning rate scheduling.
fn train_hybrid_kan<M: Module>(
model: &M,
train_x: &Tensor,
train_y: &Tensor,
vs: &nn::VarStore,
num_epochs: i64,
initial_lr: f64,
decay_rate: f64,
batch_size: i64,
) -> f64 {
let mut opt = nn::Adam {
wd: 1e-4, // Weight decay for L2 regularization
..Default::default()
}
.build(vs, initial_lr)
.unwrap();
let num_batches = train_x.size()[0] / batch_size;
for epoch in 1..=num_epochs {
let mut total_loss = 0.0;
for batch_idx in 0..num_batches {
let batch_x = train_x.narrow(0, batch_idx * batch_size, batch_size);
let batch_y = train_y.narrow(0, batch_idx * batch_size, batch_size);
let logits = model.forward(&batch_x);
let loss = logits.mse_loss(&batch_y, tch::Reduction::Mean);
opt.backward_step(&loss);
total_loss += loss.double_value(&[]);
}
let avg_loss = total_loss / num_batches as f64;
let new_lr = initial_lr * (1.0 / (1.0 + decay_rate * epoch as f64));
opt.set_lr(new_lr);
if epoch % 10 == 0 {
println!("Epoch: {} - Avg Loss: {:.6}", epoch, avg_loss);
}
}
model
.forward(&train_x)
.mse_loss(&train_y, tch::Reduction::Mean)
.double_value(&[])
}
// Evaluate the hybrid KAN model.
fn evaluate_hybrid_kan<M: Module>(model: &M, test_x: &Tensor, test_y: &Tensor) -> f64 {
let predictions = model.forward(&test_x);
predictions
.mse_loss(&test_y, tch::Reduction::Mean)
.double_value(&[])
}
fn main() {
let device = Device::cuda_if_available();
let (train_x_raw, train_y, test_x_raw, test_y) = generate_time_series_data();
let degree = 3; // Degree for polynomial basis
// Apply polynomial basis expansion to the raw data.
let train_x = polynomial_basis(&train_x_raw, degree);
let test_x = polynomial_basis(&test_x_raw, degree);
let input_dim = train_x.size()[1]; // Input dimension after polynomial basis
let hidden_dim = 64; // Number of hidden units
let output_dim = 1; // Output dimension (single value prediction)
let num_layers = 2; // Number of layers
let dropout_rate = 0.3; // Dropout rate for regularization
let num_epochs = 100;
let learning_rate = 1e-3;
let decay_rate = 0.01;
let batch_size = 32;
let vs = nn::VarStore::new(device);
let hybrid_model = hybrid_kan_model(
&vs.root(),
input_dim,
hidden_dim,
output_dim,
num_layers,
dropout_rate,
);
// Train the hybrid KAN model.
let final_loss = train_hybrid_kan(
&hybrid_model,
&train_x,
&train_y,
&vs,
num_epochs,
learning_rate,
decay_rate,
batch_size,
);
println!("Final Training Loss: {:.6}", final_loss);
// Evaluate the hybrid KAN model.
let test_mse = evaluate_hybrid_kan(&hybrid_model, &test_x, &test_y);
println!("Test Mean Squared Error: {:.6}", test_mse);
}
The code first generates synthetic time series data, adds Gaussian noise for realism, and applies polynomial basis transformations to augment features. The hybrid_kan_model function constructs the architecture, combining an LSTM layer (using tch::nn) for sequence processing and a fully connected output layer for predictions. The training process uses the Adam optimizer with weight decay (L2 regularization) and dynamically adjusts the learning rate per epoch to improve convergence. Training is performed in batches, and the loss is computed using Mean Squared Error (MSE). The evaluation step calculates the MSE on the test set, assessing the model's prediction accuracy. The architecture and workflow efficiently handle temporal and nonlinear dependencies in time series data, leveraging GPU acceleration for performance.
This example shows how KANs can be applied to time series forecasting, a common problem in finance, engineering, and scientific research. Compared to Recurrent Neural Networks (RNNs), which are often used for time series data due to their ability to capture sequential dependencies, KANs offer a different approach by focusing on the decomposition of the underlying function. This can lead to models that are simpler and more interpretable, providing insights into the structure of the time series rather than merely predicting outcomes.
However, applying KANs to larger datasets or more complex time series may require careful optimization of the model's structure and hyperparameters to balance computational complexity with accuracy. Techniques like parallel computation and Rust’s memory safety features can be leveraged to make KANs practical for real-world deployments. Moreover, their inherent interpretability can make them suitable for applications where transparency is critical, such as in regulatory environments in finance or healthcare.
Figure 4: Key challenges in scaling KAN models.
The code can be enhanced with several potential improvements. First, advanced optimizers like Cosine Annealing or Cyclical Learning Rates could be incorporated to improve convergence and adapt learning rates dynamically. Introducing an attention mechanism would allow the model to focus on key time steps in the sequence, potentially improving temporal pattern recognition. Hyperparameter tuning, such as optimizing the degree of the polynomial basis, the number of hidden units, and the number of layers, could lead to better performance. Expanding the evaluation metrics to include R-squared or Mean Absolute Error (MAE) would provide a more comprehensive assessment of the model's accuracy. Finally, implementing k-fold cross-validation would enhance model robustness by evaluating its performance across multiple splits of the dataset, reducing the risk of overfitting and ensuring generalizability.
This combined explanation and code provide a comprehensive view of how KANs can be effectively used for practical applications, highlighting their versatility and robustness in handling diverse data-driven challenges. By implementing KANs in Rust, the example demonstrates how high-performance computing can be applied to achieve both accuracy and efficiency in modeling complex functions.
18.5. Conclusion
Chapter 18 equips you with the knowledge and tools to implement and optimize Kolmogorov-Arnolds Networks using Rust. By mastering these techniques, you can build powerful models capable of accurately approximating complex functions, providing both efficiency and interpretability in high-dimensional data analysis.
18.5.1. Further Learning with GenAI
These prompts are designed to challenge your understanding of Kolmogorov-Arnolds Networks (KANs) and their implementation using Rust. Each prompt encourages deep exploration of advanced concepts, architectural innovations, and practical challenges in building and training KANs.
Analyze the theoretical foundations of Kolmogorov-Arnolds Networks. How does the Kolmogorov-Arnold representation theorem underpin the design of KANs, and how can Rust be used to implement this theorem in practice?
Discuss the trade-offs between model complexity and interpretability in KANs. How can Rust be used to explore different KAN architectures, and what are the implications for balancing performance and transparency?
Examine the role of basis functions in KANs. How can Rust be used to implement various basis functions, such as polynomial or Fourier bases, and what are the benefits of each in different applications?
Explore the challenges of training KANs on high-dimensional datasets. How can Rust be used to optimize the training process, and what strategies can be employed to ensure convergence and accuracy?
Investigate the potential of deep KANs for modeling complex functions. How can Rust be used to implement deep KAN architectures, and what are the key considerations in designing and training these models?
Discuss the importance of initialization strategies in KANs. How can Rust be used to implement effective initialization methods, and what are the impacts on model convergence and performance?
Examine the use of regularization techniques in KANs. How can Rust be used to implement regularization methods, such as weight decay or dropout, to prevent overfitting and improve model generalization?
Explore the applications of KANs in scientific computing. How can Rust be used to model complex physical systems with KANs, and what are the benefits of using these networks in scientific research?
Analyze the ethical considerations of using KANs in sensitive applications. How can Rust be used to ensure that KAN models are transparent, fair, and interpretable, particularly in domains like healthcare or finance?
Discuss the challenges of scaling KANs to large datasets. How can Rust be used to implement efficient training and inference algorithms for KANs, and what are the key bottlenecks to address?
Investigate the role of gradient-based optimization in training KANs. How can Rust be used to implement gradient descent and its variants for optimizing KAN models, and what are the trade-offs between different optimization methods?
Explore the use of KANs in time series prediction. How can Rust be used to implement KANs for forecasting tasks, and what are the advantages of KANs over traditional time series models?
Examine the potential of KANs for high-dimensional regression analysis. How can Rust be used to implement KANs for regression tasks, and what are the benefits of using KANs compared to other regression models?
Discuss the impact of learning rate schedules on KAN training. How can Rust be used to implement dynamic learning rate schedules, and what are the implications for training stability and model performance?
Analyze the effectiveness of different optimization techniques in training KANs. How can Rust be used to experiment with methods like Adam, RMSprop, or SGD, and what are the trade-offs in terms of convergence speed and accuracy?
Explore the integration of KANs with other machine learning models. How can Rust be used to combine KANs with neural networks or decision trees, and what are the potential benefits of such hybrid models?
Investigate the use of KANs in financial modeling. How can Rust be used to implement KANs for tasks like stock price prediction or risk assessment, and what are the challenges in applying KANs to financial data?
Discuss the role of hyperparameter tuning in optimizing KANs. How can Rust be used to implement hyperparameter optimization techniques, such as grid search or Bayesian optimization, for fine-tuning KAN models?
Examine the potential of KANs for unsupervised learning tasks. How can Rust be used to implement KANs for clustering or dimensionality reduction, and what are the advantages of using KANs in these contexts?
Discuss the future directions of research in Kolmogorov-Arnolds Networks. How can Rust contribute to advancements in KANs, particularly in developing new architectures, optimization methods, or applications?
By engaging with these comprehensive and challenging questions, you will develop the insights and skills necessary to build, optimize, and innovate in the field of function approximation and high-dimensional data analysis. Let these prompts inspire you to explore the full potential of KANs and push the boundaries of what is possible in AI and machine learning.
18.6.2. Hands On Practices
These exercises are designed to provide in-depth, practical experience with Kolmogorov-Arnolds Networks using Rust. They challenge you to apply advanced techniques and develop a strong understanding of implementing and optimizing KANs through hands-on coding, experimentation, and analysis.
Exercise 18.1: Implementing a Basic Kolmogorov-Arnolds Network
Task: Implement a basic KAN in Rust using the
tch-rsorcandlecrate. Decompose a simple multivariate function into its univariate components and evaluate the model’s accuracy.Challenge: Experiment with different basis functions and layer configurations. Analyze the impact of these choices on the model’s ability to approximate the target function.
Exercise 18.2: Training a Deep Kolmogorov-Arnolds Network
Task: Implement a deep KAN in Rust to model a complex, high-dimensional function. Train the model using gradient-based optimization and evaluate its performance on a regression task.
Challenge: Experiment with different optimization techniques and learning rate schedules. Analyze the convergence and accuracy of the deep KAN compared to shallow KANs and other regression models.
Exercise 18.3: Implementing Regularization Techniques in KANs
Task: Implement regularization techniques, such as weight decay or dropout, in a KAN model using Rust. Train the regularized KAN on a high-dimensional dataset and evaluate its generalization performance.
Challenge: Experiment with different regularization parameters and analyze their impact on model performance and overfitting. Compare the results with an unregularized KAN.
Exercise 18.4: Applying KANs to Time Series Forecasting
Task: Implement a KAN in Rust for time series forecasting. Train the KAN on a time series dataset, such as stock prices or weather data, and evaluate its forecasting accuracy.
Challenge: Experiment with different KAN architectures and hyperparameters. Analyze the advantages of using KANs for time series forecasting compared to traditional models like ARIMA or LSTMs.
Exercise 18.5: Building a Hybrid Model with KANs and Neural Networks
Task: Implement a hybrid model in Rust that combines a KAN with a neural network. Use the hybrid model to perform a complex regression task, leveraging the strengths of both KANs and neural networks.
Challenge: Experiment with different ways of integrating the KAN and neural network components. Analyze the performance and interpretability of the hybrid model compared to standalone KANs and neural networks.
By completing these challenges, you will gain hands-on experience and develop a deep understanding of the complexities involved in implementing and optimizing KANs, preparing you for advanced work in machine learning and AI.
Comments