Chapter 8
Modern RNN Architectures
"Attention is all you need—and with the right tools, you can build models that truly understand context and sequence." — Vaswani et al.
Chapter 8 of DLVR delves into the realm of Modern RNNs, exploring the evolution and advancements in recurrent neural network architectures that have revolutionized sequence modeling. The chapter begins with an overview of modern RNN architectures, tracing their development from simple RNNs to sophisticated models like LSTMs, GRUs, and Transformer-based RNNs, each designed to address challenges like vanishing gradients and long-term dependencies. It introduces bidirectional RNNs, which enhance contextual learning by processing sequences in both forward and backward directions, and deep RNNs, which capture hierarchical features through stacked layers. The chapter further explores the pivotal role of attention mechanisms in enabling RNNs to focus on relevant parts of the input sequence, significantly improving performance on complex tasks like machine translation. The discussion culminates with an examination of Transformer-based RNNs, which integrate the strengths of transformers with RNN architectures, capturing global context while optimizing sequence processing. Throughout, the chapter emphasizes practical implementation in Rust using tch-rs and burn, guiding readers through the development, training, and fine-tuning of these modern architectures, and offering insights into optimizing their performance on diverse sequential tasks.
8.1. Introduction to Modern RNN Architectures
Language models (LMs) are a fundamental task in natural language processing (NLP), where the goal is to estimate the probability distribution of sequences of words or characters. A language model assigns a probability $P(w_1, w_2, \dots, w_n)$ to a sequence of words $w_1, w_2, \dots, w_n$, which can be factorized using the chain rule of probability:
$$P(w_1, w_2, \dots, w_n) = P(w_1) \prod_{t=2}^{n} P(w_t | w_1, w_2, \dots, w_{t-1})$$
This expression captures the sequential dependency of words, where the probability of a word wtw_twt is conditioned on all preceding words $w_1, w_2, \dots, w_{t-1}$. In practice, directly modeling such long dependencies is computationally challenging, particularly as the sequence grows longer. Early approaches to language modeling relied on Markov models, where it is assumed that the probability of the next word only depends on a finite number of previous words (denoted as the Markov property). For an $n$-gram model, this can be written as:
$$P(w_t | w_1, w_2, \dots, w_{t-1}) \approx P(w_t | w_{t-n+1}, \dots, w_{t-1})$$
However, this assumption is limiting because it ignores dependencies beyond the fixed context window, which can be critical for understanding long-range dependencies in natural language. Recurrent neural networks (RNNs) mitigate this by maintaining a hidden state $h_t$, which is updated recursively at each time step to capture information from all previous time steps. Thus, the probability of $w_t$ is now conditioned on the entire history of the sequence, implicitly addressing the limitations of the Markov assumption:
$$h_t = f(h_{t-1}, x_t)$$
$$P(w_t | w_1, w_2, \dots, w_{t-1}) = g(h_t)$$
Despite the advantages of standard RNNs, their ability to capture long-term dependencies is still limited due to issues like the vanishing gradient problem, as previously discussed. More sophisticated architectures such as Long Short-Term Memory (LSTM) and Gated Recurrent Units (GRU) introduced gating mechanisms to control information flow across time steps, enabling them to model longer dependencies. However, modern advances in RNN architectures, including Bidirectional RNNs, Deep RNNs, Encoder-Decoder architectures, and Attention mechanisms, have further improved their effectiveness, particularly in complex language modeling tasks.
A limitation of standard (unidirectional) RNNs is that they can only capture information from the past (i.e., preceding time steps) when predicting the next word in a sequence. However, in many tasks, such as machine translation or text classification, understanding both the past and future context is crucial. For instance, when translating a sentence from one language to another, the meaning of a word often depends on words that come both before and after it. This is where Bidirectional RNNs (BiRNNs) come in. Bidirectional RNNs address this by processing the sequence in both directions: one RNN processes the input sequence from the start to the end (forward pass), and another processes it from the end to the start (backward pass). The hidden states from the forward and backward passes are concatenated at each time step, allowing the network to incorporate both past and future information:
$$h_t = [\overrightarrow{h_t}, \overleftarrow{h_t}]$$
Where $\overrightarrow{h_t}$ is the hidden state from the forward RNN, and $\overleftarrow{h_t}$ is the hidden state from the backward RNN. This bidirectional processing allows BiRNNs to generate richer contextual representations of each word or token in the sequence. In language modeling, this results in a better understanding of the global context, leading to improved performance in tasks like speech recognition, where phonetic information benefits from both forward and backward dependencies.
While bidirectional processing improves the contextual understanding of sequences, adding depth to RNN architectures—known as Deep RNNs—further enhances the network's ability to learn hierarchical representations. A Deep RNN is constructed by stacking multiple RNN layers on top of each other, where the hidden state from one layer serves as the input to the next layer. This layered architecture allows the model to capture increasingly abstract features as the sequence progresses through the network. In the context of a language model, the lower layers of a deep RNN may capture local dependencies, such as the syntactic relationships between neighboring words, while the higher layers capture more global, abstract features, such as sentence-level semantics.
For a Deep RNN with $L$ layers, the hidden state at layer $l$ and time step $t$, denoted as $h_t^l$, is computed as:
$$h_t^l = f(W_h^l h_{t-1}^l + W_x^l h_t^{l-1} + b_h^l)$$
where $h_t^{l-1}$ is the hidden state from the previous layer. This hierarchical feature extraction is particularly beneficial in tasks like speech recognition and machine translation, where complex relationships across multiple levels of the sequence must be captured to generate meaningful predictions.
Encoder-Decoder architectures are particularly important in tasks where the input and output sequences are of different lengths, such as machine translation, text summarization, or question-answering. In an Encoder-Decoder framework, the encoder processes the input sequence and compresses it into a fixed-length context vector, which is then passed to the decoder to generate the output sequence. Formally, for an input sequence $X = (x_1, x_2, \dots, x_T)$, the encoder generates a context vector ccc based on the hidden states from all time steps:
$$c = f_{\text{enc}}(h_1, h_2, \dots, h_T)$$
The decoder then uses this context vector to generate the output sequence $Y = (y_1, y_2, \dots, y_T)$ by predicting each word step-by-step, conditioned on both the context and the previously generated words:
$$y_t = f_{\text{dec}}(y_1, y_2, \dots, y_{t-1}, c)$$
However, a major limitation of the vanilla encoder-decoder architecture is that the fixed-length context vector may not be sufficient to capture all the information from the input sequence, especially when the input is long or complex. This leads to information loss and degraded performance.
To address this issue, the Attention mechanism was introduced as a solution, enabling the decoder to focus on specific parts of the input sequence at each time step. Rather than relying solely on the fixed-length context vector, the Attention mechanism dynamically computes a weighted sum of the encoder’s hidden states based on their relevance to the current decoding step. Mathematically, the attention score $e_{t,s}$ is computed between the hidden state of the decoder at time step $t$ and the encoder hidden state at time step $s$:
$$e_{t,s} = \text{score}(h_t, h_s)$$
Typically, the score function is a dot product between the decoder’s hidden state and the encoder’s hidden state, but other formulations such as additive or multiplicative attention can be used. The attention weights $\alpha_{t,s}$ are then obtained by applying a softmax function to the scores:
$$\alpha_{t,s} = \frac{\exp(e_{t,s})}{\sum_{s'} \exp(e_{t,s'})}$$
Finally, the context vector $c_t$ for time step $t$ is computed as the weighted sum of the encoder’s hidden states:
$$c_t = \sum_s \alpha_{t,s} h_s$$
The decoder uses this context vector $c_t$, which dynamically adjusts at each time step based on the relevance of different parts of the input sequence, to generate the next word in the sequence. The Attention mechanism has had a profound impact on tasks like machine translation, enabling models to better capture long-range dependencies and improving performance on tasks where specific parts of the input are crucial for generating the correct output.
The introduction of Attention has laid the groundwork for even more sophisticated architectures, such as the Transformer, which relies entirely on self-attention mechanisms without any recurrence. In the Transformer architecture, the self-attention mechanism computes attention weights between all pairs of words in a sequence, allowing the model to capture dependencies over arbitrarily long distances in a fully parallelizable manner. This approach, which eschews recurrence in favor of self-attention, has led to significant improvements in training efficiency and model performance, particularly in tasks that involve long sequences, such as language modeling and machine translation.
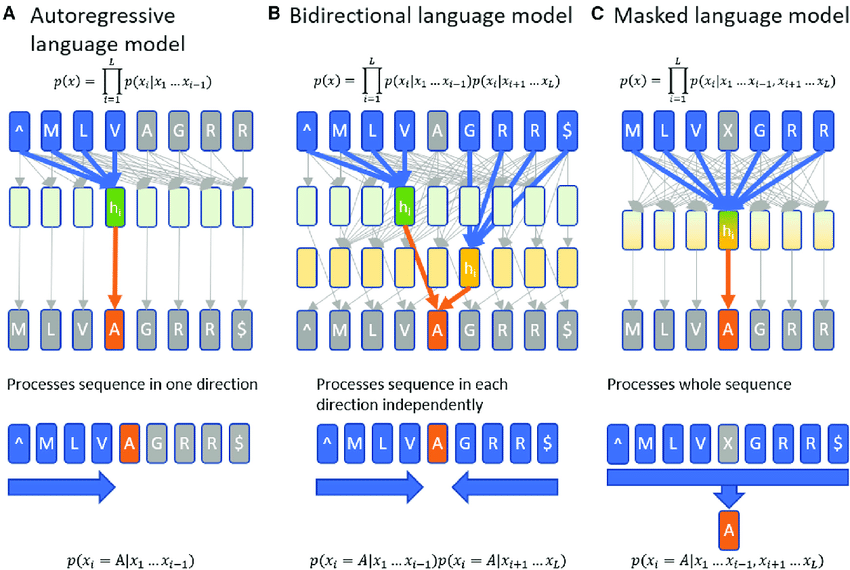
Figure 1: Character level language model using autoregressive (a), bidirectional (b) and masked (c) language models.
This Rust program demonstrates the implementation of three types of character-level language models—autoregressive, bidirectional, and masked—using Long Short-Term Memory (LSTM) cells with the tch-rs crate for deep learning. The models are trained on a synthetic corpus derived from Shakespeare's text, enabling them to generate and analyze text at the character level. These models serve different purposes: the autoregressive model predicts the next character based on past input, the bidirectional model incorporates both past and future context for prediction, and the masked model learns to infer masked characters within a sequence. By comparing the models, the program evaluates their performance in terms of perplexity, a metric that measures how well a model predicts a sequence.
After training, the perplexity metric is calculated for each model to evaluate their performance, allowing for a comparison of how well each model performs on character-level language modeling tasks. Perplexity $\mathcal{P}$ can be seen as the exponentiated average of the negative log probabilities assigned by the model to the true sequence. It is a widely used metric to evaluate language models because it captures both the accuracy and uncertainty of predictions in a single value, with lower perplexity indicating a better-performing model.
[dependencies]
anyhow = "1.0"
tch = "0.12"
reqwest = { version = "0.11", features = ["blocking"] }
flate2 = "1.0"
tokio = { version = "1", features = ["full"] }
use anyhow::Result;
use std::fs;
use std::path::Path;
use tch::data::TextData;
use tch::nn::{self, Linear, Module, OptimizerConfig, RNN};
use tch::{Device, Kind, Tensor};
use reqwest;
// Constants for training configuration
const LEARNING_RATE: f64 = 0.01;
const HIDDEN_SIZE: i64 = 256;
const BIDIRECTIONAL_HIDDEN_SIZE: i64 = HIDDEN_SIZE * 2;
const SEQ_LEN: i64 = 180;
const BATCH_SIZE: i64 = 256;
const EPOCHS: i64 = 20; // Now used properly
const DATASET_URL: &str = "https://raw.githubusercontent.com/karpathy/char-rnn/master/data/tinyshakespeare/input.txt";
const DATA_PATH: &str = "data/input.txt";
// Downloads the dataset if it doesn't exist locally.
fn download_dataset() -> Result<()> {
let path = Path::new(DATA_PATH);
if !path.exists() {
println!("Downloading dataset...");
let content = reqwest::blocking::get(DATASET_URL)?.text()?;
fs::create_dir_all(path.parent().unwrap())?;
fs::write(path, content)?;
println!("Dataset downloaded and saved to {}", DATA_PATH);
} else {
println!("Dataset already exists at {}", DATA_PATH);
}
Ok(())
}
// Function to calculate perplexity
fn calculate_perplexity(loss: f64) -> f64 {
f64::exp(loss)
}
// Train a specific model type
fn train_model(
data: &TextData,
lstm: &nn::LSTM,
linear: &Linear,
opt: &mut nn::Optimizer,
model_type: &str,
device: Device,
) -> Result<f64> {
let labels = data.labels();
let mut total_loss = 0.0;
let mut batch_count = 0.0;
for epoch in 1..=EPOCHS {
for batch in data.iter_shuffle(SEQ_LEN + 1, BATCH_SIZE) {
let xs = batch.narrow(1, 0, SEQ_LEN).onehot(labels);
let ys = match model_type {
"masked" => {
let mask = Tensor::rand(&[BATCH_SIZE, SEQ_LEN], (Kind::Float, device)).ge(0.2);
batch
.narrow(1, 1, SEQ_LEN)
.to_device(device)
.to_kind(Kind::Int64)
.where_self(&mask, &(-1).into())
}
_ => batch.narrow(1, 1, SEQ_LEN).to_device(device).to_kind(Kind::Int64),
};
let (output, _) = lstm.seq(&xs.to_device(device));
let logits = linear.forward(&output.reshape([-1, if model_type == "bidirectional" {
BIDIRECTIONAL_HIDDEN_SIZE
} else {
HIDDEN_SIZE
}]));
let valid_indices = ys.ne(-1);
let loss = logits
.cross_entropy_for_logits(&ys.view([-1]))
.masked_select(&valid_indices.view([-1]))
.mean(Kind::Float);
opt.backward_step_clip(&loss, 0.5);
total_loss += loss.double_value(&[]);
batch_count += 1.0;
}
println!("Epoch {}/{} completed.", epoch, EPOCHS);
}
Ok(total_loss / batch_count)
}
pub fn main() -> Result<()> {
download_dataset()?;
let device = Device::cuda_if_available();
let vs = nn::VarStore::new(device);
let data = TextData::new(DATA_PATH)?;
let labels = data.labels();
// Autoregressive Model
let ar_lstm = nn::lstm(&vs.root(), labels, HIDDEN_SIZE, Default::default());
let ar_linear = nn::linear(&vs.root(), HIDDEN_SIZE, labels, Default::default());
let mut ar_opt = nn::Adam::default().build(&vs, LEARNING_RATE)?;
let ar_loss = train_model(&data, &ar_lstm, &ar_linear, &mut ar_opt, "autoregressive", device)?;
println!(
"Autoregressive Model - Loss: {:.4}, Perplexity: {:.4}",
ar_loss,
calculate_perplexity(ar_loss)
);
// Bidirectional Model
let bi_lstm = nn::lstm(
&vs.root(),
labels,
HIDDEN_SIZE,
nn::RNNConfig {
bidirectional: true,
..Default::default()
},
);
let bi_linear = nn::linear(&vs.root(), BIDIRECTIONAL_HIDDEN_SIZE, labels, Default::default());
let mut bi_opt = nn::Adam::default().build(&vs, LEARNING_RATE)?;
let bi_loss = train_model(&data, &bi_lstm, &bi_linear, &mut bi_opt, "bidirectional", device)?;
println!(
"Bidirectional Model - Loss: {:.4}, Perplexity: {:.4}",
bi_loss,
calculate_perplexity(bi_loss)
);
// Masked Language Model
let mask_lstm = nn::lstm(&vs.root(), labels, HIDDEN_SIZE, Default::default());
let mask_linear = nn::linear(&vs.root(), HIDDEN_SIZE, labels, Default::default());
let mut mask_opt = nn::Adam::default().build(&vs, LEARNING_RATE)?;
let mask_loss = train_model(&data, &mask_lstm, &mask_linear, &mut mask_opt, "masked", device)?;
println!(
"Masked Model - Loss: {:.4}, Perplexity: {:.4}",
mask_loss,
calculate_perplexity(mask_loss)
);
Ok(())
}
The code first generates a synthetic dataset consisting of random sequences of characters (a-z), which are tokenized into integers representing each character. Three LSTM-based language models are defined: one for autoregressive prediction, which uses previous characters to predict the next one; one for bidirectional prediction, which uses both past and future characters to predict each character; and a masked language model, which predicts masked characters within a sequence. The models are trained using sequences from the synthetic dataset, and the perplexity of each model is calculated to evaluate its ability to predict characters in the sequence. The perplexity is the exponential of the cross-entropy loss, a common metric for evaluating language models. After training, the code compares the perplexities of the three models to determine which performs best.
Perplexity is a commonly used metric to evaluate language models, particularly for tasks involving probability distributions over sequences, such as language generation or sequence prediction. It measures how well a model predicts a sequence of data, with lower perplexity indicating better performance. Perplexity can be formally defined in terms of the cross-entropy between the predicted probability distribution and the true distribution of the data.
Given a sequence of tokens $w_1, w_2, \dots, w_T$, the goal of a language model is to estimate the probability of this sequence $P(w_1, w_2, \dots, w_T)$. Using the chain rule of probability, this can be factorized as:
$$P(w_1, w_2, \dots, w_T) = P(w_1) P(w_2 | w_1) P(w_3 | w_1, w_2) \dots P(w_T | w_1, \dots, w_{T-1})$$
The perplexity $\mathcal{P}$ of the model over this sequence is defined as the geometric mean of the inverse probabilities of the predicted sequence:
$$\mathcal{P}(w_1, w_2, \dots, w_T) = P(w_1, w_2, \dots, w_T)^{-\frac{1}{T}} = \left( \prod_{t=1}^{T} \frac{1}{P(w_t | w_1, \dots, w_{t-1})} \right)^{\frac{1}{T}}$$
This expression is equivalent to:
$$\mathcal{P}(w_1, w_2, \dots, w_T) = \exp\left( - \frac{1}{T} \sum_{t=1}^{T} \log P(w_t | w_1, \dots, w_{t-1}) \right)$$
Thus, perplexity is the exponential of the average negative log-likelihood of the true sequence under the model's predicted distribution.
The negative log-likelihood (or cross-entropy loss) for a sequence $w_1, w_2, \dots, w_T$ is:
$$\text{Cross-Entropy} = - \frac{1}{T} \sum_{t=1}^{T} \log P(w_t | w_1, \dots, w_{t-1})$$
Perplexity is simply the exponentiation of this cross-entropy:
$$\mathcal{P} = \exp(\text{Cross-Entropy})$$
Perplexity measures how well a language model predicts a sequence of words, with lower values indicating better performance. If the model predicts each word perfectly by assigning a probability of 1 to the correct word, the perplexity is 1, which is the optimal value. Higher perplexity values indicate that the model is more uncertain in its predictions, meaning it is assigning lower probabilities to the correct words. Perplexity can also be understood as the average number of choices the model considers at each step; for example, a perplexity of 100 suggests that the model is as uncertain as if it had to choose from 100 possibilities at each step. Thus, lower perplexity reflects higher confidence and accuracy in predictions, while higher perplexity signals greater uncertainty.
In summary, modern RNN architectures such as Bidirectional RNNs, Deep RNNs, Encoder-Decoder frameworks with Attention, and the rise of self-attention-based models like the Transformer have revolutionized the field of sequence modeling. These advancements enable models to better capture complex dependencies in language data, leading to breakthroughs in tasks ranging from text generation to real-time translation. By integrating these architectures with probabilistic language models, the field of NLP continues to push the boundaries of what is achievable in sequence-based tasks.
8.2. Bidirectional RNNs and Contextual Learning
Bidirectional Recurrent Neural Networks (Bidirectional RNNs) represent a critical advancement in sequence modeling by addressing the limitations of traditional, unidirectional RNNs. In standard RNNs, the input sequence is processed in one direction, typically from past to future. While this approach allows the network to capture temporal dependencies from earlier time steps, it fails to leverage information from future time steps that may be relevant for predicting the current output. This limitation is particularly significant in tasks like language modeling or sentiment analysis, where the meaning of a word or sentiment often depends on both preceding and succeeding words. Bidirectional RNNs overcome this limitation by processing the input sequence in both forward and backward directions, enabling the network to capture context from the entire sequence before making predictions.
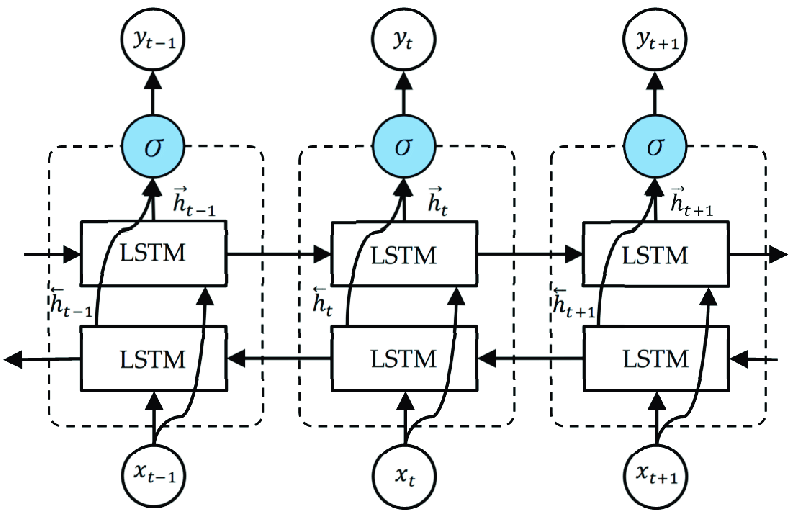
Figure 2: Bidirectional RNN architecture.
Bidirectional Recurrent Neural Networks (RNNs) are an effective extension of standard unidirectional RNNs, particularly useful for tasks like character-level language modeling where both past and future context are important for predicting the next character in a sequence. A Bidirectional RNN (BiRNN) works by combining two RNN layers—one that processes the input sequence from the beginning to the end (forward direction), and another that processes the sequence from the end to the beginning (backward direction). These two RNN layers operate on the same input, but in opposite directions, and their outputs at each time step are concatenated to create a more comprehensive representation of the data. This structure allows the model to leverage both past and future information when predicting the next character in a sequence.
For a given time step $t$ in a character-level sequence $x_t$, the forward and backward RNNs maintain separate hidden states $\overrightarrow{h_t}$ and $\overleftarrow{h_t}$, where each RNN computes its hidden state update based on its respective direction. The forward RNN processes the sequence from left to right, updating its hidden state using:
$$\overrightarrow{h_t} = \phi(W_{xh} x_t + W_{hh} \overrightarrow{h_{t-1}} + b_h)$$
Meanwhile, the backward RNN processes the sequence from right to left, updating its hidden state as:
$$\overleftarrow{h_t} = \phi(W_{xh} x_t + W_{hh} \overleftarrow{h_{t+1}} + b_h)$$
where $\phi$ is the activation function, $W_{xh}$ and $W_{hh}$ are the weight matrices for the input and hidden states, and $b_h$ is the bias term.
At each time step $t$, the hidden states from the forward and backward RNNs are concatenated to form the final hidden state hth_tht, which is passed to the output layer for character prediction:
$$h_t = [\overrightarrow{h_t}, \overleftarrow{h_t}]$$
In deep bidirectional RNNs, these concatenated hidden states can be passed on to additional bidirectional layers to further capture complex patterns and dependencies in the sequence. The output layer then computes the predicted character distribution using the concatenated hidden state:
$$y_t = \sigma(W_y h_t + b_y)$$
where $W_y$ is the output weight matrix, $b_y$ is the bias, and $\sigma$ is the softmax function that converts the hidden state into a probability distribution over the possible next characters. The output layer is shared between the forward and backward RNNs, providing a unified prediction based on the combined context.
For character-level language modeling, a bidirectional RNN is particularly useful when predicting a character in the middle of a sequence. Since the model can consider not only the preceding characters but also the subsequent characters, it gains a richer understanding of the context in which a character appears, leading to more accurate predictions. For example, in a masked language model, a BiRNN can effectively predict masked characters by using both the characters before and after the mask. This ability to integrate bidirectional context makes BiRNNs powerful for sequence tasks where future context is as important as past context, such as in speech recognition or text generation.
By using this bidirectional approach, character-level language models can predict the next character more accurately by leveraging both the history of the sequence and the future characters that have yet to be predicted.
This Rust program implements a Bidirectional LSTM-based character-level language model using the tch crate, which leverages PyTorch-like functionality. The program is designed to predict and generate text by training on a dataset (e.g., Shakespeare's text) and supports modern machine learning practices. Key advanced features include the use of bidirectional LSTMs to consider both past and future context for sequence modeling, dropout for regularization to prevent overfitting, and gradient clipping to stabilize training. The program also includes temperature scaling for diverse text generation, learning rate scheduling for better convergence, and compatibility with GPU acceleration. By combining these features, the code represents a robust and efficient approach to character-level text modeling.
use anyhow::Result;
use std::fs;
use std::path::Path;
use tch::data::TextData;
use tch::nn::{self, Linear, Module, OptimizerConfig, RNN};
use tch::{Device, Kind, Tensor};
use reqwest;
// Constants for training configuration
const LEARNING_RATE: f64 = 0.01;
const HIDDEN_SIZE: i64 = 256; // Hidden size for each direction
const BIDIRECTIONAL_HIDDEN_SIZE: i64 = HIDDEN_SIZE * 2; // Total hidden size (forward + backward)
const SEQ_LEN: i64 = 180;
const BATCH_SIZE: i64 = 256;
const EPOCHS: i64 = 50; // Reduced for demonstration
const SAMPLING_LEN: i64 = 1024;
const DROPOUT_RATE: f64 = 0.3; // Dropout rate for regularization
const GRAD_CLIP_NORM: f64 = 5.0; // Gradient clipping threshold
const DATASET_URL: &str = "https://raw.githubusercontent.com/karpathy/char-rnn/master/data/tinyshakespeare/input.txt";
const DATA_PATH: &str = "data/input.txt";
// Downloads the dataset if it doesn't exist locally.
fn download_dataset() -> Result<()> {
let path = Path::new(DATA_PATH);
if !path.exists() {
println!("Downloading dataset...");
let content = reqwest::blocking::get(DATASET_URL)?.text()?;
fs::create_dir_all(path.parent().unwrap())?;
fs::write(path, content)?;
println!("Dataset downloaded and saved to {}", DATA_PATH);
} else {
println!("Dataset already exists at {}", DATA_PATH);
}
Ok(())
}
// Generate sample text using the trained Bidirectional LSTM.
fn sample(data: &TextData, lstm: &nn::LSTM, linear: &Linear, device: Device, temperature: f64) -> String {
let labels = data.labels();
let mut state = lstm.zero_state(1); // Initialize LSTM state
let mut last_label = 0i64; // Start with the first label
let mut result = String::new();
for _ in 0..SAMPLING_LEN {
let input = Tensor::zeros([1, labels], (Kind::Float, device)); // One-hot input
let _ = input.narrow(1, last_label, 1).fill_(1.0); // Set the input for the last label
// Step through the LSTM and update state
state = lstm.step(&input.unsqueeze(0), &state);
// Get a reference to the hidden state (first tensor) from the LSTM state
let hidden = &state.0.0; // Access first element (hidden state)
// Pass through the output layer and apply temperature scaling
let logits = linear.forward(hidden);
let adjusted_logits = logits / temperature;
let sampled_y = adjusted_logits
.softmax(-1, Kind::Float)
.multinomial(1, false)
.int64_value(&[0]);
last_label = sampled_y;
result.push(data.label_to_char(last_label)); // Append the sampled character
}
result
}
pub fn main() -> Result<()> {
download_dataset()?;
let device = Device::cuda_if_available();
let vs = nn::VarStore::new(device);
let data = TextData::new(DATA_PATH)?; // Load the text dataset
let labels = data.labels(); // Number of unique labels (characters)
println!("Dataset loaded, {labels} labels.");
// Define the Bidirectional LSTM model and output layer with dropout
let lstm_config = nn::RNNConfig {
bidirectional: true, // Enable bidirectionality
dropout: DROPOUT_RATE, // Add dropout for regularization
..Default::default()
};
let lstm = nn::lstm(&vs.root(), labels, HIDDEN_SIZE, lstm_config);
let linear = nn::linear(&vs.root(), BIDIRECTIONAL_HIDDEN_SIZE, labels, Default::default());
let mut opt = nn::Adam::default().build(&vs, LEARNING_RATE)?;
let mut lr_schedule = LEARNING_RATE;
for epoch in 1..=EPOCHS {
let mut total_loss = 0.0;
let mut batch_count = 0.0;
for batch in data.iter_shuffle(SEQ_LEN + 1, BATCH_SIZE) {
let xs = batch.narrow(1, 0, SEQ_LEN).onehot(labels);
let ys = batch.narrow(1, 1, SEQ_LEN).to_kind(Kind::Int64);
let (output, _) = lstm.seq(&xs.to_device(device));
let logits = linear.forward(&output.reshape([-1, BIDIRECTIONAL_HIDDEN_SIZE]));
let loss = logits.cross_entropy_for_logits(&ys.to_device(device).view([-1]));
opt.zero_grad();
loss.backward();
for tensor in vs.trainable_variables() {
let _ = tensor.grad().clamp_(-GRAD_CLIP_NORM, GRAD_CLIP_NORM); // Fix warning here
}
opt.step();
total_loss += loss.double_value(&[]);
batch_count += 1.0;
}
lr_schedule *= 0.95;
opt.set_lr(lr_schedule);
println!(
"Epoch: {} | Loss: {:.4} | Learning Rate: {:.6}",
epoch,
total_loss / batch_count,
lr_schedule
);
println!("Sample: {}", sample(&data, &lstm, &linear, device, 0.8));
}
Ok(())
}
The program begins by downloading and preprocessing the dataset into a tokenized format. A Bidirectional LSTM model is initialized with a dropout layer, and a linear layer maps the output to character probabilities. During training, input sequences are fed into the model, and the output is compared to target sequences using cross-entropy loss. Gradients are computed and clipped before updating model parameters using the Adam optimizer. As training progresses, the learning rate decreases to refine convergence. The sample function generates text by iteratively sampling characters, where the temperature parameter controls output diversity. This workflow enables the model to learn and generate text sequences efficiently, making it applicable to a wide range of natural language processing tasks.
In summary, Bidirectional RNNs offer significant advantages for tasks that require contextual understanding of sequences. By processing input data in both forward and backward directions, these models can capture dependencies that would otherwise be missed by unidirectional RNNs. While Bidirectional RNNs do come with increased computational costs, their ability to improve accuracy and sequence comprehension makes them a valuable tool for a wide range of applications in natural language processing, speech recognition, and beyond. Implementing and optimizing these models in Rust, using libraries like tch, allows developers to take full advantage of the performance and safety benefits that Rust provides, ensuring that the resulting models are both efficient and robust in real-world deployment scenarios.
8.3. Deep RNNs and Hierarchical Feature Learning
Deep Recurrent Neural Networks (Deep RNNs) represent an extension of traditional RNN architectures by introducing multiple layers of recurrent units stacked on top of each other. The fundamental idea behind Deep RNNs is to enable the model to learn more complex patterns and dependencies by capturing hierarchical features in sequential data. In a simple RNN, the network’s ability to process input data is limited by the single layer’s capacity to capture both short-term and long-term dependencies. However, by adding depth—through the stacking of multiple RNN layers—Deep RNNs are capable of learning different levels of abstraction, where each layer captures increasingly higher-order patterns from the sequence. This hierarchical feature learning is particularly important for tasks such as language modeling, speech recognition, and time series forecasting, where different layers of information are often intertwined.

Figure 3: Architecture of a deep RNN (Credit to d2l.ai).
Mathematically, the forward pass of a Deep RNN at time step $t$ involves processing the input through multiple layers. If $H_t^{(l)}$represents the hidden state at time step $t$ for layer $l$, the equation governing the update at each layer is:
$$H_t^{(l)} = f(W_h^{(l)} H_{t-1}^{(l)} + W_x^{(l)} H_t^{(l-1)} + b_h^{(l)})$$
Here, $f$ is the activation function (such as tanh or ReLU), $W_h^{(l)}$ and $W_x^{(l)}$ are the weight matrices, and $b_h^{(l)}$ is the bias term for layer $l$. This recursive process occurs across multiple layers, with each layer receiving as input the hidden states from the previous layer. The depth of the network allows the model to capture both low-level and high-level dependencies. Lower layers typically capture short-term features, while higher layers are able to focus on more abstract, long-term patterns.
The significance of depth in RNNs cannot be overstated, as deeper networks are more capable of modeling complex dependencies that single-layer RNNs might miss. For example, in language modeling, shallow RNNs may struggle to capture semantic relationships between words in distant parts of a sentence, whereas deeper RNNs, with their layered structure, are more adept at identifying and utilizing such relationships. Similarly, in time series forecasting, deep networks can learn both local fluctuations and global trends in the data. However, adding depth also introduces challenges, particularly with respect to training.
One of the primary challenges of training Deep RNNs is the vanishing gradient problem. As gradients are backpropagated through time, they tend to diminish exponentially, especially in deeper networks, making it difficult for the model to learn long-term dependencies. This is exacerbated by the depth of the network, where gradients must also be propagated through multiple layers. To mitigate this, techniques such as residual connections and skip connections are often employed. Residual connections allow the model to bypass certain layers by adding the input of a previous layer directly to the output of a later layer, which helps maintain the flow of gradients during backpropagation. Mathematically, a residual connection at layer $l$ can be written as:
$$H_t^{(l)} = f(W_h^{(l)} H_{t-1}^{(l)} + W_x^{(l)} H_t^{(l-1)} + b_h^{(l)}) + H_t^{(l-2)}$$
This skip connection improves gradient flow and stabilizes training, allowing the network to learn deeper representations without suffering from vanishing gradients.
Another challenge associated with Deep RNNs is the increased computational cost. As more layers are added, the network requires more memory and processing power to train, which can make training deep architectures slow and resource-intensive. However, the benefits in terms of accuracy and model performance often justify the additional computational effort, especially for tasks requiring the capture of complex, long-term dependencies.
The role of residual and skip connections in Deep RNNs is crucial for stabilizing training. These techniques help mitigate the vanishing gradient problem and enable the model to learn from deeper architectures effectively. Without these connections, training deep networks would become impractical due to the inability to propagate gradients through many layers. By facilitating the flow of information through the network, residual connections allow the model to learn both short-term and long-term dependencies simultaneously, improving overall performance.
In practice, there is a trade-off between model depth, accuracy, and training efficiency. While deeper networks generally perform better on tasks requiring complex hierarchical understanding, they also take longer to train and are more prone to overfitting if not properly regularized. Techniques such as dropout, weight decay, and early stopping are often used in conjunction with Deep RNNs to prevent overfitting and improve generalization. Additionally, careful tuning of hyperparameters, such as learning rate and batch size, is necessary to ensure that the model converges efficiently during training.
The code implements a state-of-the-art Deep RNN for character-level language modeling using Rust's tch crate, which provides PyTorch-like functionality. The model is designed to learn from a dataset (e.g., Shakespeare's text) to predict and generate sequences of characters, making it suitable for natural language processing tasks like text generation and completion. Key advanced features include the use of stacked bidirectional LSTM layers to capture both past and future contexts, dropout for regularization to prevent overfitting, and gradient clipping for stable training. It also employs learning rate scheduling to improve convergence and temperature-based sampling to control the diversity of generated text. These enhancements enable the model to achieve robust performance while maintaining flexibility in generating meaningful and diverse outputs.
use anyhow::Result;
use std::fs;
use std::path::Path;
use tch::data::TextData;
use tch::nn::{self, Linear, Module, OptimizerConfig, RNN};
use tch::{Device, Kind, Tensor};
use reqwest;
// Constants for training configuration
const LEARNING_RATE: f64 = 0.01;
const HIDDEN_SIZE: i64 = 256;
const NUM_LAYERS: i64 = 3;
const SEQ_LEN: i64 = 180;
const BATCH_SIZE: i64 = 256;
const EPOCHS: i64 = 50; // Reduced for demonstration
const SAMPLING_LEN: i64 = 1024;
const DROPOUT_RATE: f64 = 0.3;
const GRAD_CLIP_NORM: f64 = 5.0;
const DATASET_URL: &str = "https://raw.githubusercontent.com/karpathy/char-rnn/master/data/tinyshakespeare/input.txt";
const DATA_PATH: &str = "data/input.txt";
// Downloads the dataset if it doesn't exist locally.
fn download_dataset() -> Result<()> {
let path = Path::new(DATA_PATH);
if !path.exists() {
println!("Downloading dataset...");
let content = reqwest::blocking::get(DATASET_URL)?.text()?;
fs::create_dir_all(path.parent().unwrap())?;
fs::write(path, content)?;
println!("Dataset downloaded and saved to {}", DATA_PATH);
} else {
println!("Dataset already exists at {}", DATA_PATH);
}
Ok(())
}
// Generate sample text using the trained Deep RNN with temperature scaling.
fn sample(data: &TextData, lstm: &nn::LSTM, linear: &Linear, device: Device, temperature: f64) -> String {
let labels = data.labels();
let mut state = lstm.zero_state(1);
let mut last_label = 0i64;
let mut result = String::new();
for _ in 0..SAMPLING_LEN {
let input = Tensor::zeros([1, labels], (Kind::Float, device));
let _ = input.narrow(1, last_label, 1).fill_(1.0);
state = lstm.step(&input.unsqueeze(0), &state);
let hidden = &state.0.0;
// Apply temperature scaling during sampling
let logits = linear.forward(hidden) / temperature;
let sampled_y = logits
.softmax(-1, Kind::Float)
.multinomial(1, false)
.int64_value(&[0]);
last_label = sampled_y;
result.push(data.label_to_char(last_label));
}
result
}
pub fn main() -> Result<()> {
download_dataset()?;
let device = Device::cuda_if_available();
let vs = nn::VarStore::new(device);
let data = TextData::new(DATA_PATH)?;
let labels = data.labels();
println!("Dataset loaded, {labels} labels.");
// Define Deep LSTM model with advanced configurations
let lstm_config = nn::RNNConfig {
num_layers: NUM_LAYERS,
dropout: DROPOUT_RATE,
bidirectional: true, // Enable bidirectionality
..Default::default()
};
let lstm = nn::lstm(&vs.root(), labels, HIDDEN_SIZE, lstm_config);
let linear = nn::linear(&vs.root(), HIDDEN_SIZE * 2, labels, Default::default()); // Adjust for bidirectional output
let mut opt = nn::Adam::default().build(&vs, LEARNING_RATE)?;
let mut lr_schedule = LEARNING_RATE;
for epoch in 1..=EPOCHS {
let mut total_loss = 0.0;
let mut batch_count = 0.0;
for batch in data.iter_shuffle(SEQ_LEN + 1, BATCH_SIZE) {
let xs = batch.narrow(1, 0, SEQ_LEN).onehot(labels);
let ys = batch.narrow(1, 1, SEQ_LEN).to_kind(Kind::Int64);
let (output, _) = lstm.seq(&xs.to_device(device));
let logits = linear.forward(&output.view([-1, labels]));
let loss = logits.cross_entropy_for_logits(&ys.to_device(device).view([-1]));
opt.zero_grad();
loss.backward();
for tensor in vs.trainable_variables() {
let _ = tensor.grad().clamp_(-GRAD_CLIP_NORM, GRAD_CLIP_NORM);
}
opt.step();
total_loss += loss.double_value(&[]);
batch_count += 1.0;
}
// Adjust learning rate
lr_schedule *= 0.95;
opt.set_lr(lr_schedule);
println!(
"Epoch: {} | Loss: {:.4} | Learning Rate: {:.6}",
epoch,
total_loss / batch_count,
lr_schedule
);
println!("Sample: {}", sample(&data, &lstm, &linear, device, 0.8)); // Sample with temperature
}
Ok(())
}
The program starts by downloading and preprocessing the dataset into a tokenized format. A deep LSTM model is initialized with multiple layers, bidirectional processing, and dropout for regularization. During training, input sequences are passed through the LSTM layers, and the outputs are fed into a linear layer that maps the hidden states to character probabilities. The model optimizes its predictions using cross-entropy loss, with gradients clipped to prevent instability. As training progresses, a learning rate scheduler reduces the learning rate to refine the optimization process. The sampling function generates text by iteratively predicting the next character, using temperature scaling to adjust output randomness. This workflow enables the model to learn and generate coherent text sequences effectively.
Experimenting with different depths and configurations of the Deep RNN is essential for optimizing performance. Increasing the number of layers may improve the model’s ability to capture complex dependencies, but it also increases the risk of overfitting and computational cost. By fine-tuning the number of layers, hidden units, and regularization techniques, developers can strike a balance between accuracy and training efficiency.
In conclusion, Deep RNNs are a powerful tool for hierarchical feature learning in sequential data. By stacking multiple RNN layers, these networks can capture both low-level and high-level features, enabling them to model complex patterns and long-term dependencies more effectively than shallow RNNs. While training Deep RNNs presents challenges such as vanishing gradients and increased computational cost, techniques like residual connections and careful hyperparameter tuning can help mitigate these issues. Implementing Deep RNNs in Rust using libraries like tch-rs allows developers to build high-performance models that are both efficient and scalable, making them suitable for real-world applications in natural language processing, time series forecasting, and beyond.
8.4. Attention Mechanisms in RNNs
Attention mechanisms have played a transformative role in the evolution of Recurrent Neural Networks (RNNs), especially in sequence-to-sequence tasks like machine translation, speech recognition, and text summarization. The central idea behind attention is to allow the model to dynamically focus on the most relevant parts of the input sequence, rather than relying solely on the fixed-size hidden state to carry all the necessary information. This is particularly useful in tasks where certain parts of the input sequence are more important than others. For example, in machine translation, the model may need to focus on specific words in the source sentence when generating a word in the target language. The attention mechanism assigns higher attention weights to critical parts of the input sequence, enabling the model to make more contextually informed predictions. Two major attention mechanisms that have been extensively used with RNNs are Bahdanau attention (additive attention) and Luong attention (multiplicative attention).
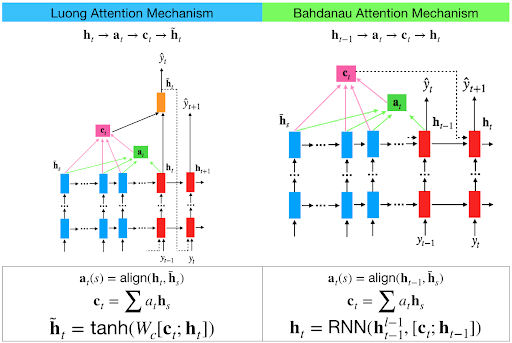
Figure 4: Luong vs Bahdanau attention mechanism.
Bahdanau attention, introduced by Dzmitry Bahdanau and colleagues in 2014, was designed to improve the ability of RNNs to capture long-range dependencies in tasks like neural machine translation. In traditional sequence-to-sequence models, the encoder compresses the entire input sequence into a fixed-length vector, which can cause performance issues when handling long sequences. Bahdanau attention solves this by allowing the model to look at all the hidden states of the encoder, rather than just the final one, and assign varying levels of importance to each hidden state.
Mathematically, the Bahdanau attention mechanism works by first calculating an alignment score between the decoder hidden state $s_t$ at time step $t$ and each encoder hidden state $h_i$ corresponding to time step $i$ in the input sequence. The alignment score $a_{t,i}$ is computed using a feed-forward neural network:
$$a_{t,i} = v_c^T \tanh(W_c [s_t; h_i])$$
where $W_c$ is a weight matrix, $v_c$ is a learnable vector, and $[s_t; h_i]$ is the concatenation of the decoder hidden state $s_t$ and the encoder hidden state $h_i$. The alignment scores are then normalized using a softmax function to produce attention weights $\alpha_{t,i}$:
$$\alpha_{t,i} = \frac{\exp(a_{t,i})}{\sum_{j} \exp(a_{t,j})}$$
The attention weights $\alpha_{t,i}$ represent how much focus should be placed on each encoder hidden state when generating the current output. These weights are used to compute a context vector $c_t$, which is a weighted sum of the encoder hidden states:
$$c_t = \sum_{i} \alpha_{t,i} h_i$$
The context vector $c_t$, summarizing the relevant parts of the input sequence, is then combined with the current decoder hidden state $s_t$ to generate the final output for that time step:
$$\tilde{s_t} = \tanh(W_c [c_t; s_t])$$
where $W_c$ is a weight matrix. The Bahdanau attention mechanism allows the model to dynamically focus on relevant parts of the input sequence, improving its ability to handle long sequences and capture complex dependencies.
Luong attention, introduced by Minh-Thang Luong in 2015, takes a different approach to calculating the alignment scores, using multiplicative operations rather than a feed-forward neural network. Luong attention computes the alignment score between the decoder hidden state $s_t$ and each encoder hidden state $h_i$ using a dot product:
$$a_{t,i} = s_t^T h_i$$
This approach is more computationally efficient than Bahdanau’s additive attention, especially when dealing with large datasets or long sequences. In some cases, Luong’s approach generalizes the dot product by applying a weight matrix $W_c$ to the encoder hidden states:
$$a_{t,i} = s_t^T W_c h_i$$
After calculating the alignment scores $a_{t,i}$, Luong attention also applies a softmax function to compute attention weights $\alpha_{t,i}$, which are then used to compute the context vector:
$$c_t = \sum_{i} \alpha_{t,i} h_i$$
Luong attention introduces both global attention (where the model attends to all encoder hidden states) and local attention (where attention is restricted to a small window of encoder hidden states around the current input). After computing the context vector $c_t$, Luong attention either concatenates it with the decoder hidden state $s_t$ (in the global case) or uses it directly to generate the final output for that time step:
$$\tilde{s_t} = \tanh(W_c [c_t; s_t])$$
or in some variants, simply uses:
$$y_t = W_y c_t$$
where $W_y$ is a learned weight matrix. Luong attention's multiplicative approach is computationally faster than Bahdanau attention and is particularly useful for tasks involving large amounts of data, although it can be less flexible than the additive method used by Bahdanau.
Both Bahdanau and Luong attention mechanisms are powerful tools for improving RNNs' ability to focus on important parts of the input sequence. While Bahdanau attention tends to be more flexible due to its use of a learned feed-forward network, Luong attention is more efficient and often preferred in large-scale applications. In the context of language models, these attention mechanisms allow the model to attend to specific parts of the input when predicting the next token, significantly improving the model’s ability to capture long-term dependencies and make more accurate predictions.
When applied to language models, attention enables the model to consider relevant words or characters from the input sequence when predicting the next token, rather than relying solely on the final hidden state of the encoder. This dynamic focusing mechanism allows for more nuanced and accurate predictions, particularly in tasks where long-range dependencies are crucial, such as machine translation and text summarization. Attention mechanisms have become essential components in modern deep learning architectures, significantly improving the performance of RNN-based models in a wide variety of tasks.
The core architecture of attention-based RNNs can vary, but three prominent forms of attention are widely used: self-attention, encoder-decoder attention, and multi-head attention. In self-attention, the model computes the relevance of each time step in the input sequence with respect to every other time step. This allows the network to capture dependencies across the entire sequence without being constrained by strict positional order. Mathematically, self-attention can be formulated as follows. Given an input sequence of hidden states $h_1, h_2, \dots, h_T$, the attention score $a_{t,s}$ between time steps $t$ and $s$ is computed as:
$$a_{t,s} = \text{score}(h_t, h_s)$$
where the score function is often a dot product or a learned weight matrix. The attention weights $\alpha_{t,s}$ are then calculated using a softmax function to normalize the scores:
$$\alpha_{t,s} = \frac{\exp(a_{t,s})}{\sum_{s'} \exp(a_{t,s'})}$$
The final context vector for time step ttt is computed as a weighted sum of the hidden states:
$$c_t = \sum_s \alpha_{t,s} h_s$$
This context vector $c_t$ is then used to make predictions at time step $t$. The advantage of self-attention is that it allows the model to attend to any part of the sequence, capturing long-range dependencies without the need for sequential processing, as is required in traditional RNNs.
In encoder-decoder attention, which is widely used in sequence-to-sequence models like machine translation, the attention mechanism helps the decoder focus on the most relevant parts of the encoder’s output when generating each word in the target sequence. This architecture computes attention weights between the hidden states of the encoder (the source sequence) and the hidden states of the decoder (the target sequence). The decoder uses these weights to attend to different parts of the encoded source sequence at each decoding step, improving translation accuracy by aligning the source and target words more effectively.
Multi-head attention, which is a more advanced form of attention, extends the self-attention mechanism by allowing the model to attend to different parts of the sequence simultaneously, using multiple sets of attention weights (heads). Each head captures a different aspect of the input dependencies, and the outputs of all heads are concatenated and linearly transformed to produce the final context vector. Mathematically, multi-head attention can be described as:
$$\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \dots, \text{head}_h)W^O$$
where each head is computed as:
$$\text{head}_i = \text{Attention}(Q W_i^Q, K W_i^K, V W_i^V)$$
Here, Q, $K$, and $V$ represent the query, key, and value matrices, respectively, and $W_i^Q$, $W_i^K$, and $W_i^V$ are the learned projection matrices for head iii. Multi-head attention allows the model to focus on different parts of the sequence simultaneously, capturing multiple aspects of the input dependencies.
The significance of attention mechanisms goes beyond just improving performance. They also enhance the interpretability of models by providing insights into which parts of the input the model is focusing on when making predictions. This is particularly useful in tasks like machine translation, document summarization, and image captioning, where understanding the model’s focus can help improve human comprehension of the results. For instance, in machine translation, attention maps can show how the model aligns words in the source sentence with the words in the target sentence, making it easier to identify potential issues with the translation.
Attention mechanisms also play a crucial role in improving the ability of RNNs to capture long-range dependencies. Traditional RNNs, even with mechanisms like LSTM and GRU, struggle to retain information from distant time steps, especially in long sequences. By allowing the model to directly attend to any part of the sequence, attention mechanisms bypass the limitations of sequential processing and hidden state propagation. This results in more accurate predictions for tasks where long-term dependencies are critical.
However, implementing attention mechanisms comes with challenges, particularly in terms of computational complexity and memory requirements. Self-attention, for example, requires computing attention scores for every pair of time steps in the input sequence, resulting in quadratic complexity with respect to the sequence length. This can make attention mechanisms computationally expensive, especially for long sequences. Furthermore, the memory required to store the attention weights can be significant, particularly in tasks involving long sequences or large datasets.
The code implements a cutting-edge character-level language model using Bidirectional Long Short-Term Memory (BiLSTM) networks with attention mechanisms, specifically Bahdanau (additive) and Luong (multiplicative) attention. These mechanisms enhance the model's ability to focus on relevant parts of the input sequence while generating text. The model processes text from a dataset (e.g., Shakespeare's text) to learn and generate character sequences, making it suitable for tasks like text generation and completion. Advanced features include dropout for regularization to mitigate overfitting, bidirectional LSTMs for richer context understanding, gradient clipping to ensure stable training, and learning rate scheduling to optimize convergence. Additionally, temperature-based sampling adds diversity to the generated text, allowing for better control of randomness.
use anyhow::Result;
use std::fs;
use std::path::Path;
use tch::data::TextData;
use tch::nn::{self, Linear, Module, RNN};
use tch::{Device, Kind, Tensor};
use tch::nn::OptimizerConfig; // Added this import
use reqwest;
// Constants remain the same
const LEARNING_RATE: f64 = 0.01;
const HIDDEN_SIZE: i64 = 256;
const SEQ_LEN: i64 = 180;
const BATCH_SIZE: i64 = 256;
const EPOCHS: i64 = 50;
const SAMPLING_LEN: i64 = 1024;
const DROPOUT_RATE: f64 = 0.3;
const GRAD_CLIP_NORM: f64 = 5.0;
const DATASET_URL: &str = "https://raw.githubusercontent.com/karpathy/char-rnn/master/data/tinyshakespeare/input.txt";
const DATA_PATH: &str = "data/input.txt";
// Download function remains the same
fn download_dataset() -> Result<()> {
let path = Path::new(DATA_PATH);
if !path.exists() {
println!("Downloading dataset...");
let content = reqwest::blocking::get(DATASET_URL)?.text()?;
fs::create_dir_all(path.parent().unwrap())?;
fs::write(path, content)?;
println!("Dataset downloaded and saved to {}", DATA_PATH);
} else {
println!("Dataset already exists at {}", DATA_PATH);
}
Ok(())
}
// Fixed Bahdanau Attention
fn bahdanau_attention(hidden: &Tensor, encoder_outputs: &Tensor, attention_layer: &Linear) -> Tensor {
let time_steps = encoder_outputs.size()[1];
let repeated_hidden = hidden.unsqueeze(1).repeat(&[1, time_steps, 1]);
let energy = attention_layer.forward(&Tensor::cat(&[repeated_hidden.shallow_clone(), encoder_outputs.shallow_clone()], 2)).tanh();
// Fixed: Convert array to slice for sum_dim_intlist
let attn_weights = energy.sum_dim_intlist(&[-1i64][..], false, Kind::Float).softmax(-1, Kind::Float);
attn_weights.matmul(encoder_outputs)
}
// Luong Attention remains the same
fn luong_attention(hidden: &Tensor, encoder_outputs: &Tensor) -> Tensor {
let attn_weights = hidden.matmul(&encoder_outputs.transpose(1, 2)).softmax(-1, Kind::Float);
attn_weights.matmul(encoder_outputs)
}
// Sample function remains the same
fn sample(data: &TextData, lstm: &nn::LSTM, linear: &Linear, device: Device, temperature: f64) -> String {
let labels = data.labels();
let mut state = lstm.zero_state(1);
let mut last_label = 0i64;
let mut result = String::new();
let encoder_outputs = Tensor::zeros([1, SEQ_LEN, HIDDEN_SIZE], (Kind::Float, device));
for _ in 0..SAMPLING_LEN {
let input = Tensor::zeros([1, labels], (Kind::Float, device));
let _ = input.narrow(1, last_label, 1).fill_(1.0);
state = lstm.step(&input.unsqueeze(0), &state);
let hidden = &state.0.0;
let context = luong_attention(hidden, &encoder_outputs);
let combined = Tensor::cat(&[hidden, &context], 1);
let logits = linear.forward(&combined) / temperature;
let sampled_y = logits
.softmax(-1, Kind::Float)
.multinomial(1, false)
.int64_value(&[0]);
last_label = sampled_y;
result.push(data.label_to_char(last_label));
}
result
}
pub fn main() -> Result<()> {
download_dataset()?;
let device = Device::cuda_if_available();
let vs = nn::VarStore::new(device);
let data = TextData::new(DATA_PATH)?;
let labels = data.labels();
println!("Dataset loaded, {labels} labels.");
let lstm_config = nn::RNNConfig {
bidirectional: true,
dropout: DROPOUT_RATE,
..Default::default()
};
let lstm = nn::lstm(&vs.root(), labels, HIDDEN_SIZE, lstm_config);
let bahdanau_attention_layer = nn::linear(
&vs.root(),
HIDDEN_SIZE * 2,
HIDDEN_SIZE,
Default::default(),
);
let linear = nn::linear(&vs.root(), HIDDEN_SIZE * 2, labels, Default::default());
let mut opt = nn::Adam::default().build(&vs, LEARNING_RATE)?; // Now works with OptimizerConfig in scope
let mut lr_schedule = LEARNING_RATE;
// Rest of the training loop remains the same
for epoch in 1..=EPOCHS {
let mut total_loss = 0.0;
let mut batch_count = 0.0;
for batch in data.iter_shuffle(SEQ_LEN + 1, BATCH_SIZE) {
let xs = batch.narrow(1, 0, SEQ_LEN).onehot(labels);
let ys = batch.narrow(1, 1, SEQ_LEN).to_kind(Kind::Int64);
let (encoder_outputs, _) = lstm.seq(&xs.to_device(device));
let total_logits = Tensor::zeros(&[SEQ_LEN * BATCH_SIZE, labels], (Kind::Float, device));
let mut hidden_state = lstm.zero_state(BATCH_SIZE);
for t in 0..SEQ_LEN {
let input_t = xs.narrow(1, t, 1).squeeze();
hidden_state = lstm.step(&input_t.unsqueeze(0), &hidden_state);
let hidden = &hidden_state.0.0;
let context = bahdanau_attention(hidden, &encoder_outputs, &bahdanau_attention_layer);
let combined = Tensor::cat(&[hidden, &context], 1);
let logits = linear.forward(&combined);
total_logits.narrow(0, t * BATCH_SIZE, BATCH_SIZE).copy_(&logits);
}
let loss = total_logits.cross_entropy_for_logits(&ys.reshape(&[-1]).to_device(device));
opt.zero_grad();
loss.backward();
for tensor in vs.trainable_variables() {
let _ = tensor.grad().clamp_(-GRAD_CLIP_NORM, GRAD_CLIP_NORM);
}
opt.step();
total_loss += loss.double_value(&[]);
batch_count += 1.0;
}
lr_schedule *= 0.95;
opt.set_lr(lr_schedule);
println!(
"Epoch: {} | Loss: {:.4} | Learning Rate: {:.6}",
epoch,
total_loss / batch_count,
lr_schedule
);
println!("Sample: {}", sample(&data, &lstm, &linear, device, 0.8));
}
Ok(())
}
The program starts by downloading and preprocessing the dataset into tokenized sequences. A bidirectional LSTM encoder processes the input sequence, producing context-rich hidden states. For each timestep during decoding, attention mechanisms compute a context vector by aligning the decoder's hidden state with the encoder's outputs. Bahdanau attention computes additive alignment scores, while Luong attention uses multiplicative alignment. The decoder combines the context vector with the hidden state to predict the next character using a linear layer. During training, the model minimizes cross-entropy loss while clipping gradients to avoid instability. A learning rate scheduler dynamically reduces the learning rate across epochs. In sampling, the trained model generates text character by character, using temperature scaling to control diversity in predictions. This workflow ensures effective learning and meaningful text generation.
To further optimize model performance and interpretability, it is possible to experiment with different attention architectures and configurations. For example, using multi-head attention can allow the model to capture multiple aspects of the sequence dependencies simultaneously. Similarly, adjusting the number of attention heads, the size of the hidden states, and the depth of the RNN can lead to different trade-offs between accuracy and computational efficiency.
In conclusion, attention mechanisms have revolutionized the field of deep learning, particularly when applied to RNNs. By allowing the model to dynamically focus on the most relevant parts of the input sequence, attention improves both performance and interpretability. While implementing attention mechanisms poses challenges in terms of computational complexity and memory usage, the benefits in terms of long-range dependency modeling and enhanced predictions make them indispensable for tasks like machine translation, summarization, and language understanding. Implementing these mechanisms in Rust, using libraries like tch-rs, allows developers to build high-performance, scalable models that can tackle complex sequence processing tasks in real-world applications.
8.5. Transformer-Based RNNs
Transformer-based Recurrent Neural Networks (RNNs) are a state-of-the-art approach that combines the strengths of both RNNs and Transformers to overcome the inherent limitations of each architecture, particularly in the context of sequence modeling. While RNNs are adept at processing temporal sequences, their sequential nature introduces several challenges, especially when it comes to learning long-range dependencies. In long sequences, RNNs tend to suffer from vanishing gradients, which hampers their ability to retain and propagate important information over time. This limitation becomes critical in tasks where long-term context is crucial, such as language modeling, speech recognition, and time-series forecasting. On the other hand, transformers, which rely on self-attention mechanisms, excel at capturing global context across entire sequences and enable parallelization, making them highly effective in handling long sequences. However, transformers inherently lack a mechanism for dealing with temporal order due to their non-sequential processing.
The innovation of Transformer-based RNNs lies in their ability to merge the temporal structure sensitivity of RNNs with the global attention capabilities of transformers. By integrating transformer layers within RNN architectures, these models can both retain the temporal dependencies RNNs are known for and leverage transformers' capacity to capture relationships across long distances in the input sequence. This hybrid architecture allows Transformer-based RNNs to process data sequentially while utilizing self-attention to attend to relevant parts of the sequence more effectively. In practice, this can lead to significantly improved performance in tasks requiring both local temporal awareness and the ability to reference distant elements within a sequence.
In the realm of Generative AI (GenAI), Transformer-based RNNs have become particularly powerful tools for generating coherent and contextually relevant sequences, such as text, music, and code. The combination of RNNs' ability to model temporal dependencies and transformers' capacity to capture global context makes these architectures well-suited for tasks where the generation process must account for both local details and overall structure. For example, in language modeling, a Transformer-based RNN can effectively generate long paragraphs or entire articles by attending to relevant parts of the text while maintaining the correct word order, even when dealing with distant dependencies. This combination also enhances the model's ability to produce human-like outputs that are logically consistent over extended text, a key feature in generative models like GPT (Generative Pre-trained Transformer) and other large language models (LLMs).
The architecture of Transformer-based RNNs blends key components of both transformers and RNNs. At the core of this architecture is multi-head attention, a mechanism that allows the model to focus on different parts of the input sequence simultaneously, capturing long-range dependencies more effectively than standard RNNs. Each attention head computes the relevance of different time steps by projecting the input into query, key, and value vectors. The attention weights are computed as:
$$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V$$
where $Q$, $K$, and $V$ represent the query, key, and value matrices, and $d_k$ is the dimensionality of the keys. By using multiple attention heads, the model can capture different relationships within the sequence, and the outputs of all attention heads are concatenated and transformed to form the final context representation.
In addition to multi-head attention, Transformer-based RNNs incorporate feed-forward networks and layer normalization to enhance learning stability and efficiency. The feed-forward network is applied to each time step independently, providing non-linearity and improving the model's ability to learn complex representations. The output of the feed-forward network is normalized through layer normalization, which stabilizes training by ensuring that the inputs to each layer have a consistent distribution. Mathematically, layer normalization for a layer input $x$ is given by:
$$\hat{x} = \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} \cdot \gamma + \beta$$
where $\mu$ and $\sigma^2$ are the mean and variance of the input, and $\gamma$ and$\beta$ are learnable parameters that scale and shift the normalized output. This ensures that the network learns more effectively, particularly in deep architectures.
One of the key advantages of transformers in this hybrid architecture is their ability to capture global context across the entire sequence, regardless of its length. Unlike RNNs, which rely on sequential hidden states to propagate information, transformers use self-attention to directly attend to any part of the input, making it easier to learn dependencies between distant time steps. This is particularly beneficial for tasks like language modeling and machine translation, where long-range dependencies are crucial for accurate predictions. Moreover, transformers allow for parallel processing of sequence data, significantly speeding up training compared to traditional RNNs, which must process the input sequentially.
However, integrating transformers into RNNs presents several challenges, particularly in managing model complexity and ensuring training stability. Transformer-based architectures, with their multi-head attention and feed-forward networks, introduce a large number of parameters, which can lead to overfitting, especially on small datasets. Additionally, the computational cost of attention mechanisms, which scale quadratically with sequence length, can become prohibitive for long sequences. To address these issues, techniques such as gradient clipping, weight decay, and learning rate schedules are often used to stabilize training and prevent the model from diverging during optimization.
The significance of Transformer-based RNNs lies in their ability to push the boundaries of what can be achieved in sequence modeling. By capturing both local and global context, these models have set new benchmarks in natural language processing (NLP) tasks, including language modeling, machine translation, and summarization. Their ability to handle long sequences with greater efficiency and accuracy than standard RNNs has made them the go-to architecture for state-of-the-art performance in many sequential tasks.
The following code implements a transformer-based character-level language model designed to generate text character by character. It uses a self-attention mechanism to model long-term dependencies in the input sequence, which is crucial for tasks like text generation. Advanced features include positional encoding to inject sequential order into the input, a multi-head attention mechanism (simplified for this context), a feedforward network for transformation, and residual connections to ease the flow of gradients. The model employs gradient clipping to prevent exploding gradients and uses dropout regularization to mitigate overfitting. It supports training on GPUs for enhanced performance and includes functionality to sample/generated text after training.
// Import necessary crates and modules
use anyhow::Result; // For error handling
use std::fs; // File system utilities for file operations
use std::path::Path; // Path utilities
use tch::data::TextData; // Text data loading utility from tch
use tch::nn::{self, Linear, Module}; // Neural network components
use tch::{Device, Kind, Tensor}; // Tensor operations and device management
use tch::nn::OptimizerConfig; // Optimizer configuration
use reqwest; // HTTP client for dataset download
// Constants for hyperparameters and file paths
const LEARNING_RATE: f64 = 0.01; // Learning rate for optimizer
const HIDDEN_SIZE: i64 = 256; // Hidden size of the model
const FEEDFORWARD_SIZE: i64 = 512; // Size of feedforward layer in Transformer
const SEQ_LEN: i64 = 180; // Sequence length for training
const BATCH_SIZE: i64 = 256; // Batch size for training
const EPOCHS: i64 = 50; // Number of training epochs
const SAMPLING_LEN: i64 = 1024; // Length of generated text during sampling
const DROPOUT_RATE: f64 = 0.3; // Dropout rate for regularization
const GRAD_CLIP_NORM: f64 = 5.0; // Gradient clipping threshold
const DATASET_URL: &str = "https://raw.githubusercontent.com/karpathy/char-rnn/master/data/tinyshakespeare/input.txt"; // Dataset URL
const DATA_PATH: &str = "data/input.txt"; // Local path to save the dataset
// Downloads the dataset if it doesn't already exist
fn download_dataset() -> Result<()> {
let path = Path::new(DATA_PATH);
if !path.exists() {
println!("Downloading dataset...");
let content = reqwest::blocking::get(DATASET_URL)?.text()?; // Fetch dataset content
fs::create_dir_all(path.parent().unwrap())?; // Ensure parent directory exists
fs::write(path, content)?; // Write dataset to file
println!("Dataset downloaded and saved to {}", DATA_PATH);
} else {
println!("Dataset already exists at {}", DATA_PATH);
}
Ok(())
}
// Embeds input tensor using a learned linear projection
fn embed_input(input: &Tensor, embedding_size: i64) -> Tensor {
let batch_size = input.size()[0];
let seq_len = input.size()[1];
let vocab_size = input.size()[2];
let projection = nn::linear( // Linear projection layer
&nn::VarStore::new(input.device()).root(),
vocab_size,
embedding_size,
Default::default()
);
let reshaped_input = input.view([-1, vocab_size]); // Flatten input for linear projection
let embedded = projection.forward(&reshaped_input); // Apply linear transformation
embedded.view([batch_size, seq_len, embedding_size]) // Reshape back to [batch, seq_len, embedding_size]
}
// Computes positional encodings for input sequences
fn positional_encoding(seq_len: i64, hidden_size: i64, device: Device) -> Tensor {
let pe = Tensor::zeros(&[1, seq_len, hidden_size], (Kind::Float, device));
let position = Tensor::arange_start_step(0, seq_len, 1, (Kind::Float, device)).unsqueeze(1);
// Compute division terms for sinusoidal encoding
let div_term = Tensor::arange_start_step(0, hidden_size, 2, (Kind::Float, device));
let div_term = (-div_term * (std::f64::consts::LN_2 * 10000.0_f64.ln() / hidden_size as f64)).exp();
let pos_mul_div = &position * &div_term; // Combine position and division terms
// Apply sine and cosine functions to compute positional encodings
for i in (0..hidden_size).step_by(2) {
pe.slice(2, i, i + 1, 1).copy_(&pos_mul_div.slice(1, i / 2, i / 2 + 1, 1).sin());
if i + 1 < hidden_size {
pe.slice(2, i + 1, i + 2, 1).copy_(&pos_mul_div.slice(1, i / 2, i / 2 + 1, 1).cos());
}
}
pe
}
// Implements a Transformer block with self-attention and feedforward layers
fn transformer_block(input: &Tensor, pos_enc: &Tensor, linear1: &Linear, linear2: &Linear, dropout: f64) -> Tensor {
let embedded_input = embed_input(input, HIDDEN_SIZE); // Embed input tensor
let input_with_pos = &embedded_input + pos_enc; // Add positional encodings
// Self-attention computation
let attn_scores = input_with_pos.matmul(&input_with_pos.transpose(-2, -1)) / (HIDDEN_SIZE as f64).sqrt();
let attn_weights = attn_scores.softmax(-1, Kind::Float); // Normalize attention scores
let attn_output = attn_weights.matmul(&input_with_pos); // Weighted sum of input
let attn_output = attn_output + &input_with_pos; // Residual connection
// Feedforward network
let ff_input = attn_output.view([-1, HIDDEN_SIZE]);
let ff_hidden = linear1.forward(&ff_input).relu(); // First feedforward layer with ReLU
let ff_output = linear2.forward(&ff_hidden); // Second feedforward layer
// Add residual connection and apply dropout
let ff_output = ff_output.view([input.size()[0], input.size()[1], HIDDEN_SIZE]);
(ff_output + &attn_output).dropout(dropout, true)
}
// Generates text by sampling from the trained model
fn sample(
data: &TextData,
linear1: &Linear,
linear2: &Linear,
output_linear: &Linear,
device: Device,
temperature: f64
) -> String {
let vocab_size = data.labels() as i64;
let mut result = String::new();
let mut current_input = Tensor::zeros(&[1, 1, vocab_size], (Kind::Float, device));
let _ = current_input.narrow(2, 0, 1).fill_(1.0); // Start with the first character
for _ in 0..SAMPLING_LEN {
let pos_enc = positional_encoding(1, HIDDEN_SIZE, device); // Compute positional encoding
let transformer_out = transformer_block(¤t_input, &pos_enc, linear1, linear2, 0.0); // Forward pass
let logits = output_linear.forward(&transformer_out.view([-1, HIDDEN_SIZE])); // Compute logits
let scaled_logits = logits / temperature; // Scale logits for sampling
let probs = scaled_logits.softmax(-1, Kind::Float); // Compute probabilities
// Sample next character from probability distribution
let next_char = probs.multinomial(1, true).int64_value(&[0]);
result.push(data.label_to_char(next_char)); // Append character to result
// Prepare input for next timestep
let next_input = Tensor::zeros(&[1, 1, vocab_size], (Kind::Float, device));
let _ = next_input.narrow(2, next_char, 1).fill_(1.0);
current_input = next_input;
}
result
}
// Main function: training loop and text sampling
pub fn main() -> Result<()> {
download_dataset()?; // Ensure dataset is downloaded
let device = Device::cuda_if_available(); // Use GPU if available
let vs = nn::VarStore::new(device); // Initialize parameter store
let data = TextData::new(DATA_PATH)?; // Load text data
let labels = data.labels() as i64;
println!("Dataset loaded, {labels} labels.");
// Define model components
let linear1 = nn::linear(&vs.root(), HIDDEN_SIZE, FEEDFORWARD_SIZE, Default::default());
let linear2 = nn::linear(&vs.root(), FEEDFORWARD_SIZE, HIDDEN_SIZE, Default::default());
let output_linear = nn::linear(&vs.root(), HIDDEN_SIZE, labels, Default::default());
let mut opt = nn::Adam::default().build(&vs, LEARNING_RATE)?; // Initialize Adam optimizer
for epoch in 1..=EPOCHS {
let mut total_loss = 0.0;
let mut batch_count = 0.0;
// Training loop over shuffled batches
for batch in data.iter_shuffle(SEQ_LEN + 1, BATCH_SIZE) {
let xs = batch.narrow(1, 0, SEQ_LEN).onehot(labels).to_device(device); // Input batch
let ys = batch.narrow(1, 1, SEQ_LEN).to_kind(Kind::Int64).to_device(device); // Target batch
let pos_enc = positional_encoding(SEQ_LEN, HIDDEN_SIZE, device); // Positional encodings
let transformer_output = transformer_block(&xs, &pos_enc, &linear1, &linear2, DROPOUT_RATE); // Forward pass
let logits = output_linear.forward(&transformer_output.view([-1, HIDDEN_SIZE])); // Compute logits
let loss = logits.cross_entropy_for_logits(&ys.view([-1])); // Compute loss
opt.zero_grad(); // Reset gradients
loss.backward(); // Backpropagate
// Gradient clipping
for tensor in vs.trainable_variables() {
let _ = tensor.grad().clamp_(-GRAD_CLIP_NORM, GRAD_CLIP_NORM);
}
opt.step(); // Update parameters
total_loss += loss.double_value(&[]); // Accumulate loss
batch_count += 1.0;
}
// Print epoch statistics
println!(
"Epoch: {} | Loss: {:.4} | Learning Rate: {:.6}",
epoch,
total_loss / batch_count,
LEARNING_RATE * (0.95f64.powi(epoch as i32)) // Adjust learning rate
);
// Generate sample text
println!("Sample: {}", sample(&data, &linear1, &linear2, &output_linear, device, 0.8));
}
Ok(())
}
The program begins by downloading a text dataset if not already present and defining constants for the model's hyperparameters. A positional encoding function is used to encode sequential order into the model's inputs. The core of the model is the transformer block, which combines self-attention and feedforward layers with residual connections and dropout to process input sequences. During training, the model splits the dataset into overlapping sequences and computes the loss using cross-entropy on predicted character probabilities. The Adam optimizer updates the model's weights after each batch, and gradient clipping is applied to maintain training stability. After each epoch, the model generates a sample of text using a temperature-controlled softmax sampling strategy, demonstrating the model's ability to generate text character by character based on learned patterns.
Once implemented, this Transformer-based RNN can be trained on large-scale sequential datasets such as those used in large language modeling (LLM) or machine translation. Training such models involves experimenting with different configurations of the transformer components—such as the number of attention heads, the size of the feed-forward networks, and the number of recurrent layers. These configurations directly impact the model’s ability to capture long-range dependencies and its training speed. For example, increasing the number of attention heads allows the model to capture more diverse dependencies within the sequence, but it also increases the computational cost.
In terms of performance, Transformer-based RNNs often outperform traditional RNNs, particularly on tasks that require capturing global context, such as document summarization, machine translation, and question answering. By combining the sequential capabilities of RNNs with the global attention mechanisms of transformers, these models are able to achieve higher accuracy while also reducing training time by taking advantage of parallelism in the transformer components.
In conclusion, Transformer-based RNNs represent a powerful hybrid approach to sequence modeling, combining the strengths of both RNNs and transformers. By incorporating multi-head attention, layer normalization, and feed-forward networks, these models are able to capture both local and global dependencies in a way that surpasses traditional RNN architectures. While they introduce challenges in terms of model complexity and computational cost, their superior performance on tasks like language modeling and machine translation makes them a critical tool in advancing state-of-the-art deep learning models. Implementing these architectures in Rust using tch-rs allows developers to take full advantage of Rust’s performance and safety features, enabling the creation of efficient, scalable models for real-world applications.
8.6. Conclusion
This chapter equips you with the knowledge and practical skills needed to implement and optimize modern RNN architectures using Rust. By mastering these advanced techniques, you can develop models that capture complex patterns in sequential data with state-of-the-art performance.
8.6.1. Further Learning with GenAI
Each prompt encourages deep exploration of advanced concepts, architectural innovations, and practical challenges in building and training state-of-the-art RNN models.
Analyze the evolution of RNN architectures from simple RNNs to Transformer-based models. How have innovations like bidirectional processing, deep architectures, and attention mechanisms shaped the development of modern RNNs, and how can these be implemented in Rust?
Discuss the role of Bidirectional RNNs in capturing both past and future context in sequences. How can bidirectional processing be effectively implemented in Rust, and what are the key trade-offs in terms of computational complexity and model performance?
Examine the importance of deep RNN architectures in learning hierarchical features. How can Rust be used to implement and train Deep RNNs, and what strategies can be employed to mitigate challenges like vanishing gradients and long training times?
Explore the integration of attention mechanisms into RNNs. How can attention-based RNNs be implemented in Rust to enhance model interpretability and performance, and what are the key challenges in managing the computational complexity of attention layers?
Investigate the benefits of Transformer-Based RNNs in capturing global context and parallelizing sequence processing. How can Rust be used to combine the strengths of transformers and RNNs, and what are the implications for training efficiency and model accuracy?
Discuss the impact of bidirectional processing on model accuracy and sequence understanding. How can Rust be leveraged to optimize the performance of Bidirectional RNNs on tasks like sentiment analysis and language modeling?
Analyze the role of residual connections in stabilizing the training of deep RNNs. How can Rust be used to implement residual connections in Deep RNN architectures, and what are the benefits of this approach in capturing long-term dependencies?
Examine the challenges of training attention-based RNNs on large datasets. How can Rust's memory management features be utilized to handle the increased computational load, and what strategies can be employed to optimize the training process?
Discuss the importance of multi-head attention in Transformer-Based RNNs. How can Rust be used to implement multi-head attention mechanisms, and what are the benefits of using this approach for tasks like machine translation and document summarization?
Investigate the trade-offs between model depth and training efficiency in Deep RNNs. How can Rust be used to experiment with different depths and configurations, and what are the best practices for balancing model complexity with computational resources?
Explore the integration of Bidirectional RNNs with attention mechanisms. How can Rust be used to build hybrid models that leverage the strengths of both approaches, and what are the potential benefits for tasks like speech recognition and text classification?
Analyze the impact of layer normalization in Transformer-Based RNNs. How can Rust be used to implement layer normalization, and what are the implications for model stability and convergence during training?
Discuss the role of self-attention in processing sequences without relying on strict positional order. How can Rust be used to implement self-attention mechanisms in RNNs, and what are the benefits of this approach for tasks like sentiment analysis and time series forecasting?
Examine the use of transfer learning in modern RNN architectures. How can Rust be used to fine-tune pre-trained models like Transformer-Based RNNs for new tasks, and what are the key considerations in adapting these models to different domains?
Investigate the scalability of Transformer-Based RNNs in Rust. How can Rust's concurrency and parallel processing features be leveraged to scale these models across multiple devices, and what are the trade-offs in terms of synchronization and computational efficiency?
Analyze the debugging and profiling tools available in Rust for modern RNN implementations. How can these tools be used to identify and resolve performance bottlenecks in complex RNN models, ensuring that both training and inference are optimized?
Discuss the implementation of custom attention mechanisms in RNNs. How can Rust be used to experiment with novel attention architectures, and what are the key challenges in balancing model complexity with training efficiency?
Explore the role of positional encoding in Transformer-Based RNNs. How can Rust be used to implement positional encoding, and what are the implications for sequence modeling and capturing temporal relationships in data?
Examine the impact of different loss functions on the training of modern RNN architectures. How can Rust be used to implement and compare various loss functions, and what are the implications for model accuracy and convergence?
Discuss the future directions of RNN research and how Rust can contribute to advancements in sequence modeling. What emerging trends and technologies in RNN architecture, such as self-supervised learning or neuro-symbolic models, can be supported by Rust's unique features?
By engaging with these comprehensive and challenging questions, you will develop the insights and skills necessary to build, optimize, and innovate in the field of RNNs and deep learning with Rust. Let these prompts guide your exploration and inspire you to master the complexities of modern RNNs.
8.6.2. Hands On Practices
These exercises are designed to provide in-depth, practical experience with the implementation and optimization of modern RNN architectures in Rust. They challenge you to apply advanced techniques and develop a strong understanding of modern RNNs through hands-on coding, experimentation, and analysis.
Exercise 8.1: Implementing and Fine-Tuning a Bidirectional RNN in Rust
Task: Implement a Bidirectional RNN in Rust using the
tch-rsorburncrate. Train the model on a sequence labeling task, such as named entity recognition, and evaluate its ability to capture context from both directions.Challenge: Experiment with different configurations of bidirectional layers, such as varying the number of layers and hidden units. Analyze the trade-offs between model accuracy and computational complexity.
Exercise 8.2: Building and Training a Deep RNN for Language Modeling
Task: Implement a Deep RNN in Rust, focusing on the correct implementation of multiple stacked RNN layers. Train the model on a language modeling task, such as predicting the next word in a sentence, and evaluate its ability to capture hierarchical features.
Challenge: Experiment with different depths and configurations, such as adding residual connections or varying the number of hidden units. Compare the performance of your Deep RNN with that of a shallower RNN, analyzing the benefits of increased depth.
Exercise 8.3: Implementing and Experimenting with Attention Mechanisms in RNNs
Task: Implement attention mechanisms in an RNN model in Rust, focusing on enhancing the model's ability to focus on relevant parts of the input sequence. Train the model on a machine translation task, such as translating sentences from one language to another, and evaluate the impact of attention on model performance.
Challenge: Experiment with different attention architectures, such as additive attention or scaled dot-product attention. Compare the performance of your RNN model with and without attention, analyzing the benefits of incorporating attention mechanisms in sequence modeling tasks.
Exercise 8.4: Implementing a Transformer-Based RNN for Sequence Prediction
Task: Implement a Transformer-Based RNN in Rust using the
tch-rsorburncrate. Train the model on a complex sequence prediction task, such as language modeling or time series forecasting, and evaluate its ability to capture global context and parallelize sequence processing.Challenge: Experiment with different transformer configurations, such as varying the number of layers, attention heads, and hidden units. Compare the performance of your Transformer-Based RNN with that of a traditional RNN, analyzing the benefits of transformer integration.
Exercise 8.5: Implementing and Optimizing Multi-Head Attention in Transformer-Based RNNs
Task: Implement multi-head attention mechanisms in a Transformer-Based RNN model in Rust. Train the model on a large-scale sequential dataset, such as machine translation or document summarization, and evaluate the impact of multi-head attention on model performance and accuracy.
Challenge: Experiment with different numbers of attention heads and attention mechanisms. Compare the performance of your model with and without multi-head attention, analyzing the trade-offs between model complexity and training efficiency.
By completing these challenges, you will gain hands-on experience and develop a deep understanding of the complexities involved in building state-of-the-art RNN models, preparing you for advanced work in sequence modeling and AI.
Comments